در این فیلم آموزشی به چگونگی حل معادله به کمک تغییر متغیر و نکات آن خواهیم پرداخت.
حل معادله به کمک تغییر متغیر
بعضی معادلات بعد از تغییر متغیر تبدیل به معادلات درجه 2 می شوند که قابل حل خواهند بود.
در معادلات درجه دوم، اگر دو حالت خاص وجود داشته باشد، معادلات را با راه حل کوتاه تری می توان حل نمود.
نکته: در حل معادلات درجه دوم ax2+bx+c=0 به دو نکته زیر توجه کنید. با کمک این نکات می توانید، ریشه های معادله را به راحتی به دست آورید.

مثال) جواب های معادله 17x2-30x+13=0 را به دست آورید؟
در معادله بالا، مجموع ضرایب صفر است، بنابراین یکی از ریشه ها 1 و 13/17دیگری است.
به حل مثال دیگری می پردازیم:
مثال) جواب های معادله 119x2+120x+1=0 را به دست آورید؟
در معادله مذکور a+c=b است. لذا یکی از ریشه ها 1- و ریشه دیگر 1/119 – می باشد.
بعضی معادلات بعد از تغییر متغیر تبدیل به معادلات درجه 2 می شوند که قابل حل خواهند بود.
در معادلات درجه دوم، اگر دو حالت خاص وجود داشته باشد، معادلات را با راه حل کوتاه تری می توان حل نمود.
نکته: در حل معادلات درجه دوم ax2+bx+c=0 به دو نکته زیر توجه کنید. با کمک این نکات می توانید، ریشه های معادله را به راحتی به دست آورید.
نکته: برای حل معادلات به فرم ax4+bx2+c=0 ( معادلات دو مجذوری) با فرض x2=t ، معادله به فرم at2+bt+c=0 یعنی درجه 2 خواهد شد. حال معادله قابل حل خواهد بود و ریشه ها را تعیین می کنیم.
مثال) ریشه های معادله 3x4-22x2+19=0 را به دست آورید؟
در ابتدا x2=t را قرار داده و معادله به فرم 3t2-22t+19=0 در خواهد آمد. حال معادله درجه دوم را حل می نمائیم. در معادله مذکور، مجموع ضرایب صفر است، پس ریشه ها به صورت زیر می باشد.
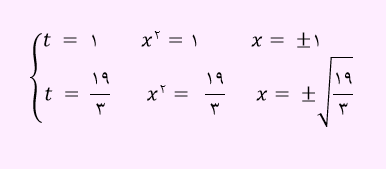
برخی معادلات بالاتر از درجه دوم، را می توان به تغییر متغیر به معادله درجه دو تبدیل نمود و سپس آن را حل کرد.
نمونه تست حل معادله به کمک تغییر متغیر
در این بخش برای درک بهتر موضوع حل معادله درجه دوم به کمک تغییر متغیر به حل نمونه تست می پردازیم.
تست) یکی از ریشه های معادله 5×2+(2m-3)x-2m-2=0 درجه دوم برابر کدام است؟
- 2m-3/5
- 2m+2/5
- 2m+2/-5
- 3-2m/5
گزینه 3 پاسخ صحیح می باشد.
در معادله مذکور، جمع ضرایب یعنی 5+(2m-3)+2m-2 – برابر با صفر می باشد. بنابراین یکی از ریشه ها 1 و ریشه دیگر برابر با c/a یعنی 2m-2/5 – است. لذا گزینه 3 پاسخ صحیح می باشد.
به منظور آشنایی بیشتر با موضوع حل معادله با کمک تغییر متغیر و حل معادلات دو مجذوری می توانید ویدئو آموزشی را مشاهده کنید.
سوالات متداول
در معادله درجه دوم، اگر مجموع ضرایب صفر باشد، یکی از ریشه ها برابر با یک و ریشه دیگر c/a می باشد.
در معادله درجه دوم ax2+bx+c=0 ، اگر a+c=b شود، ریشه ها برابر با 1- و c/a





