در این فیلم آموزشی با موضوع حل معادله درجه دوم به کمک اتحاد جمله مشترک و ریشه گیری آشنا خواهید شد.
طبق اتحاد جمله مشترک می دانیم، جملات به فرم زیر به شکل بیان شده تجزیه خواهند شد:
بنابراین با توجه به عبارت بالا ریشه های معادله یافت خواهند شد.
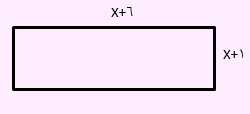
تست اول) اگر مساحت مستطیل زیر برابر 24 باشد. محیط این مستطیل کدام است؟
1- 22
2- 20
3- 50
4- 28
گزینه 1 پاسخ صحیح می باشد.
مساحت این مستطیل به صورت زیر محاسبه خواهد شد:
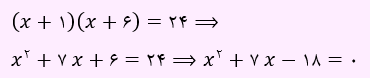
حال با توجه به اتحاد جمله مشترک، دو عدد می یابیم که حاصل ضرب آن ها برابر با 18- و جمع آن ها مساوی با 7 شود.
با توجه به اینکه طول مستطیل نمی تواند منفی باشد، ریشه -9 غیر قابل قبول است. بنابراین طول و عرض مستطیل برابر با 8 و 3 خواهد شد. حال محیط مستطیل را به صورت زیر محاسبه خواهیم کرد:
لذا محیط مستطیل برابر با 22 به دست آمد.
ریشه گیری، یکی از روش های حل معادله درجه دوم می باشد.
حل معادله درجه دوم به کمک ریشه گیری: برای حل معادله درجه دوم به کمک ریشه گیری به صورت زیر عمل خواهیم کرد:
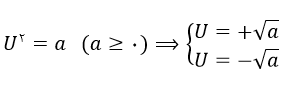
مثال) معادله زیر را حل کنید؟
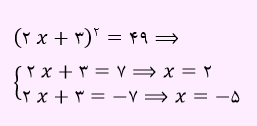
طبق نکته ریشه گیری معادله بالا را حل نموده ایم.
برای آشنایی بیشتر با موضوع حل معادله درجه دوم به کمک اتحاد جمله مشترک، ریشه گیری و نمونه سوالات آن می توانید ویدئو آموزشی را مشاهده کنید.
به منظور حل معادله درجه دوم می توان از اتحاد جمله مشترک و روش ریشه گیری استفاده نمود.
برای حل معادلات درجه دوم به روش اتحاد جمله مشترک، ابتدا جمله مشترک را می یابیم. سپس دو عدد که ضرب و جمع آن ها برابر با ضریب جمله مشترک و عدد تنها شود را پیدا می کنیم و طبق آن اتحاد جمله مشترک را می نویسیم. در نهایت منفی آن دو عدد یافت شده برابر با ریشه های معادله خواهند شد.
فرض کنید توان دوم یک عبارت برابر با مقدار مثبتی باشد. برای حل معادله به روش ریشه گیری، عبارت را برابر با منفی و مثبت رادیکال آن مقدار مثبت قرار خواهیم داد.
مؤسسه آموزشی فرهنگی گزینهدو برگزارکننده آزمون آزمایشی ویژۀ داوطلبان آزمون سراسری و آزمون‌های استاندارد ارزشیابی پیشرفت تحصیلی در دورۀ اول متوسطه و پایه‌های دهم و یازدهم می‌باشد. گزینهدو به‌عنوان یک مؤسسه پیشرو در زمینه خدمات نوین آموزشی، نرم‌افزارهای گوناگونی را جهت بهبود فرآیند آموزش و سنجش برای دانش‌آموزان و مدارس ارائه می‌کند.
مؤسسه آموزشی فرهنگی گزینهدو برگزارکننده آزمون آزمایشی ویژۀ داوطلبان آزمون سراسری و آزمون‌های استاندارد ارزشیابی پیشرفت تحصیلی در دورۀ اول متوسطه و پایه‌های دهم و یازدهم می‌باشد. گزینهدو به‌عنوان یک مؤسسه پیشرو در زمینه خدمات نوین آموزشی، نرم‌افزارهای گوناگونی را جهت بهبود فرآیند آموزش و سنجش برای دانش‌آموزان و مدارس ارائه می‌کند.
