در این فیلم آموزشی با موضوع تعمیم قضیه تالس، نکات تستی و کنکوری آن آشنا خواهید شد.
تعمیم قضیه تالس
تعمیم قضیۀ تالس: اگر خطی دو ضلع مثلثی را در دو نقطه قطع کند و با ضلع سوم آن موازی باشد، مثلثی پدید می آید که اندازۀ اضلاع آن با اندازۀ اضلاع مثلث اصلی متناسب اند:


تعمیم قضیه تالس، یکی از قضیه های مهم برای حل مسائل هندسی می باشد.
نمونه تست تعمیم قضیه تالس
به نمونه تست زیر دقت کنید:
تست: در مثلث ABC، اندازه AB=3 و AC=6 است. نقاط D، E و F روی اضلاع طوری قرار گرفته اند که ADEF یک لوزی است. طول ضلع این لوزی کدام است؟

1- 2
2- 2.5
3- 3
4- 3.5
پاسخ : گزینه 1 پاسخ صحیح می باشد.
در لوزی ضلع ها با یکدیگر موازی هستند.یعنی ضلع AD با EF و ضلع DE با AF موازی می باشد. همچنین هر چهار ضلع لوزی با یکدیگر مساوی هستند. بنابراین مطابق با شکل زیر داریم:

حال با توجه به تعمیم قضیه تالس داریم:

بنابراین مقدار a برابر با 1 به دست آمد.
به تست دوم توجه فرمایید:
تست: در مثلث قائم الزاویۀ ABC به طول اضلاع 3، 4 و 5، روی دو ضلع AB و AC دو مربع بنا کرده ایم. مطابق شکل، مجموع AM+AN کدام است؟

1- 12/7
2- 3
3- 24/7
4- 4
پاسخ : گزینه 3 پاسخ صحیح می باشد.

در مثلث BED، ضلع AM با ED و در مثلث FGC، ضلع AN با FG موازی است لذا از تعمیم تالس مطابق با روابط زیر استفاده خواهیم کرد:
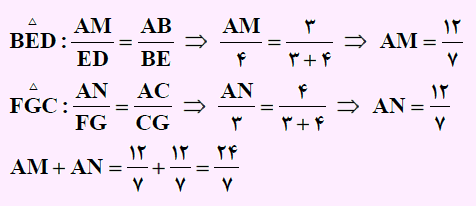
بنابراین مقدار AM+AN برابر با 24/7 به دست آمد.
به منظور مشاهده نمونه تست های بیشتر در مورد موضوع تعمیم قضیه تالس و نکات آن می توانید به ویدئو آموزشی مراجعه کنید.
سوالات متداول
اگر خطی دو ضلع مثلثی را در دو نقطه قطع کند و با ضلع سوم آن موازی باشد، مثلثی پدید می آید که اندازۀ اضلاع آن با اندازۀ اضلاع مثلث اصلی متتناسب اند، که به آن تعمیم قضیه تالس گفته خواهد شد.
بله، در صورت مشاهده خطوط موازی در مثلث، می توان از تعمیم قضیه تالس استفاده نمود.





