در این فیلم آموزشی در مورد موضوع قضیه تالس، عکس قضیه تالس و تعمیم این قضیه توضیح داده شده است.
قضیه تالس
اگر خطی به موازات یک ضلع مثلث رسم و دو ضلع دیگر را قطع کند، روی آن دو ضلع پاره خط های متناسب ایجاد خواهد کرد.
در واقع، در شکل مقابل MN با BC موازی است و رابطه های زیر برقرار می باشد. به رابطه های مذکور قضیه تالس گفته خواهد شد.
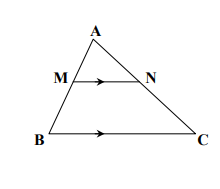

مثال: در شکل مقابل MN با BC موازی می باشد. نسبت MN/BC کدام است؟

بر اساس قضیه تالس، نسبت زیر برقرار است.
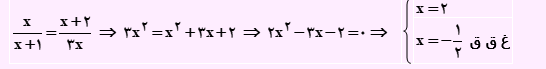
x=-1/2 غیر قابل قبول است. چون طول نمی تواند منفی باشد.
نسبت MN/BC بر اساس قضیه تالس با AM/AB برابر است . پس رابطه زیر را داریم.
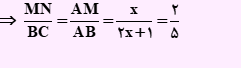
به نمونه تست زیر توجه کنید:
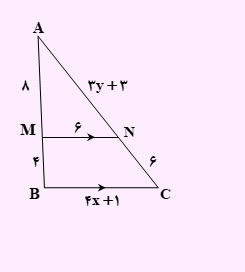
تست) با توجه به شکل مقابل، x + y کدام است. (پاره خط MN با BC موازی است)؟
- 5
- 6
- 8
- 4
گزینه 1 پاسخ صحیح می باشد.
با توجه به اینکه پاره خط MN با BC موازی است، قضیه تالس برقرار است. بنابراین رابطه زیر را خواهیم داشت.
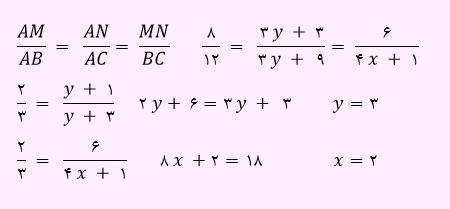
پس مقدار x + y برابر با 5 خواهد شد.
در مسائل مربوط به ذوزنقه که یک خط موازی با قاعده رسم می شود، با رسم قطر ذوزنقه و دوبار استفاده از قضیه تالس می توان مسائی معمولی را حل نمود. برای آشنایی با تست این موضوع می توانید ویدئو آموزشی را مشاهده کنید.
قضیه تالس بیان می کند اگر خطی به موازات یک ضلع مثلث رسم و دو ضلع دیگر را قطع کند، روی آن دو ضلع پاره خط های متناسب ایجاد خواهد کرد.
تعمیم قضیه تالس و عکس قضیه تالس
تعمیم قضیه تالس: در شکل مقابل خطوط d1، d2 و d3 موازی یکدیگرند، در این صورت داریم:

مثال: در شکل مقابل، خطوط d1 ، d2 و d3 موازیند، مقدار m کدام است؟
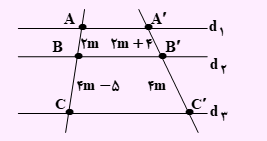
با توجه به تعمیم قضیه تالس داریم:
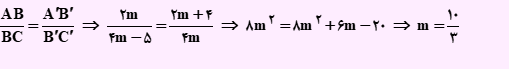
عکس قضیه تالس : اگر در مثلث شکل زیر تناسب بیان شده برقرار باشد، آن گاه خطوط MN و BC با یکدیگر موازی هستند.

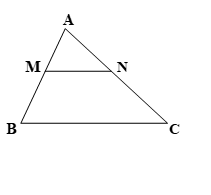
به منظور آشنایی بیشتر با قضیه تالس، تعمیم قضیه تالس و عکس آن می توانید ویدئو آموزشی را مشاهده کنید.
سوالات متداول
اگر یک سری خطوط موازی رسم شود و دو خط این خطوط موازی را قطع کند، روی دو خط مذکور پاره خط های متناسب ایجاد خواهد شد.
اگر خطی به موازات یک ضلع مثلث رسم کنیم و آن خط دو ضلع دیگر مثلث را قطع کند، آن گاه خط مذکور روی آن دو ضلع، پاره خط های متناسب ایجاد می کند.





