در این فیلم آموزشی به موضوع توابع نمایی، معرفی دامنه و برد آن ها خواهیم پرداخت.
تابع نمایی: تابع با ضابطه f(x)=ax که a>0 و a≠1 را تابع نمایی می نامیم. به عنوان مثال تابع y=3x ، تابع نمایی می باشند.
دامنه تابع نمایی y=ax برابر R و برد آن (∞+, 0) است.
در حالتی که a>1 باشد، تابع افزایشی ( صعودی) و در حالتی که a بین صفر و یک باشد ، تابع کاهشی ( نزولی) است.
در هر دو حالت ذکر شده ، تابع یک به یک و معکوس پذیر است.
نمودار تابع نمایی در شکل زیر نشان داده شده است:
نکته : برای مقایسه نمودار توابع نمایی می توان از روابط زیر کمک گرفت.
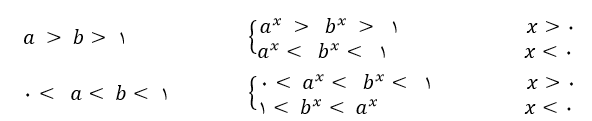
دامنه تابع نمایی برابر با R می باشد.
در این بخش به حل نمونه تست در مورد توابع نمایی می پردازیم.
تست) اگر دو تابع f(x)=3×9x و g(x)=2(1/3)2x-5 در نقطه A متقاطع باشند. عرض نقطه A کدام است؟
گزینه 1 پاسخ صحیح می باشد.
باید دو تابع f (x) و g(x) را با یکدیگر برابر قرار دهیم. بنابراین روابط زیر را خواهیم داشت.
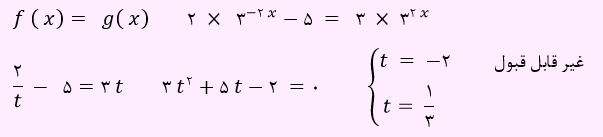
چون برد تابع نمایی اعداد مثبت است، t=-2 غیر قابل قبول می باشد.
بنابراین روابط زیر را خواهیم داشت.
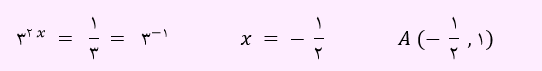
در روابط بالا، پایه ها را یکسان نمودیم و سپس نماها باید برابر باشند. لذا عرض نقطه A برابر با 1 می شود. بنابراین گزینه 1 پاسخ صحیح می باشد.
به منظور یادگیری بیشتر موضوع تابع نمایی و نکات آن ویدئو آموزشی را مشاهده کنید.
بله. لازم به ذکر است تابع نمایی، در تمام حالات یک به یک و معکوس پذیر خواهد بود.
تابع نمایی در مواردی که a>1 باشد، یک تابع صعوی و در واقع افزایشی می باشد و در مواردی که a بین صفر و یک باشد، تابع نمایی یک تابع نزولی و در حقیقت کاهشی خواهد بود.
موسسه آموزشی فرهنگی گزینه دو برگزارکننده آزمون آزمایشی ویژه داوطلبان آزمون سراسری و آزمون های استاندارد ارزشیابی پیشرفت تحصیلی در دوره اول متوسطه و پایه های دهم و یازدهم می باشد. گزینه دو به عنوان یک موسسه پیشرو در زمینه خدمات نوین آموزشی، نرم افزارهای گوناگونی را جهت بهبود فرآیند آموزش و سنجش برای دانش آموزان و مدارس ارائه می کند
