در این فیلم آموزشی با نکاتی از قوانین گزاره ها، جبر گزاره ها، گزاره های مرکب، تعریف ریاضی ترکیب دو شرطی،گزاره های همیشه درست و معروف، گزاره های همیشه نادرست و معروف، تعریف ریاضی ترکیب شرطی و نقیض آن، نقیض ترکیب دو شرطی، عکس نقیض ترکیب شرطی آشنا خواهید شد.
تعریف ریاضی ترکیب دو شرطی
تعریف ریاضی ترکیب دو شرطی به صورت زیر می باشد:
قوانین دمورگان به قوانین زیر گفته می شود:
در قوانین دمورگان، هنگامی که نقیض روی ترکیب عطفی یا فصلی اثر می کند، ترکیب عطفی را به فصلی و ترکیب فصلی را به عطفی تبدیل خواهد کرد و هر دو گزاره نقیض می شوند.
تست اول) گزاره چنین نیست که ” در مستطیل قطرها برابر نیست یا عدد 4 مربع کامل است” معادل است با:
الف) در مستطیل قطرها برابر است یا 4 مربع کامل نیست.
ب) در مستطیل قطرها برابر است و 4 مربع کامل نیست.
ج) در مستطیل قطرها برابر نیست و 4 مربع کامل نیست.
د) در مستطیل قطرها برابر نیست یا 4 مربع کامل نیست.
گزینه ب پاسخ صحیح می باشد.
در صورت سوال گفته شده ” چنین نیست”، بنابراین منظور نقیض است. با توجه به قانون دمورگان “یا” به “و” تبدیل خواهد شد و هر کدام از گزاره ها نقیض می شوند. یعنی نقیض گزاره مذکور برابر با ” در مستطیل قطرها برابر است و 4 مربع کامل نیست.” می باشد.
به نمونه تست دوم توجه فرمایید:
تست دوم) اگر داشته باشیم “10√ عدد گنگ است : p” و ” 25 مضرب 3 نیست : q” گزاره ( p ∧ q) ∼ به کدام صورت است؟
الف) 10√ عددی گنگ نیست و 25 مضرب 3 است.
ب) 10√ عددی گنگ نیست و 25 مضرب 3 نیست.
ج) 10√ گویا است یا 25 مضرب 3 است.
د) 10√ گویا است و 25 مضرب 3 نیست.
گزینه ج پاسخ صحیح می باشد.
بر اساس قانون دمورگان، ( p ∧q) ∼= p ∨ ∼q ∼، می باشد. بنابراین جواب سوال مساوی با ” 10√عددی گنگ نیست یا 25 مضرب 3 است.” خواهد شد. این عبارت معادل با ” √10 گویا است یا 25 مضرب 3 است.” می باشد.
قوانین دمورگان با اثر کردن نقیض روی ترکیب عطفی یا فصلی، ترکیب عطفی را به فصلی و ترکیب فصلی را به عطفی تبدیل می کند.
تعریف ریاضی ترکیب شرطی و نقیض آن
گزار های زیر، گزاره های معروفی هستند که همیشه درست هستند.

تعریف ریاضی ترکیب شرطی و نقیض آن به صورت زیر خواهد بود:

نقیض ترکیب دو شرطی و عکس نقیض ترکیب شرطی به صورت زیر است:

عکس نقیض ترکیب شرطی با خود ترکیب شرطی هم ارز است.
در اثبات برخی احکام ریاضی برای سهولت در اثبات، به جای خود گزاره شرطی، عکس نقیض آن را ثابت می کنیم.
مثال) برای اثبات حکم ” اگر a ϵ Z و a2 زوج باشد، آن گاه a نیز زوج است” ثابت می کنیم: “اگر a زوج نباشد آن گاه a2 زوج نیست” یعنی ” اگر a فرد باشد، a2 نیز فرد است”
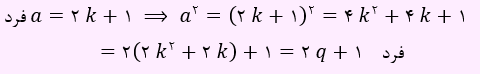
در واقع در اثبات از عکس نقیض استفاده کردیم.
به منظور مشاهده نمونه تست های بیشتر در مورد موضوع تعریف ریاضی ترکیب شرطی و ترکیب و شرطی به ویدئو آموزشی توجه فرمایید.
سوالات متداول
تعریف ریاضی ترکیب شرطی و نقیض آن به شکل زیر می باشد:
p ⟹q ≡ ∼p ∨q
(p ⟹q) ∼≡p ∧ ∼q
تعریف ریاضی ترکیب دو شرطی به شکل زیر خواهد بود:
p ⟺q ≡( p ⟹q) ∧ (q ⟹p) ≡ ∼p ⟺ ∼q
عکس نقیض ترکیب شرطی به صورت زیر می باشد:
q ⟹ ∼p ≡p ⟹q ∼





