در این فیلم آموزشی با موضوع روابط طولی در دایره ها و نکات تستی آن آشنا خواهید شد.
روابط طولی در دایره ها
نکتۀ 1: اگر دو وتر دلخواه AB و CD در نقطۀ M داخل دایره متقاطع باشند، داریم:

نکتۀ 2: اگر دو وتر دلخواه AB و CD در نقطۀ M خارج دایره متقاطع باشند، داریم:

MT مماس بر دایره در نقطۀ M است.
روابط طولی در دایره بسیار مهم می باشد.
نمونه تست روابط طولی در دایره
به نمونه تست زیر دقت کنید:
تست (سراسری 92): در دایرهای به قطر 12 واحد، فاصلۀ مرکز دایره از وتر AB برابر 2 است. نقطۀ C در امتداد AB به فاصلۀ CB=2√2 انتخاب شده است. طول قطعۀ مماسی که از C بر دایره رسم شود، کدام است؟
1- 10√2
2- 5√3
3- 7
4- 2√5
پاسخ : گزینه 1 پاسخ صحیح می باشد.
با توجه به موارد گفته شده در صورت سوال، شکل به صورت زیر خواهد بود:
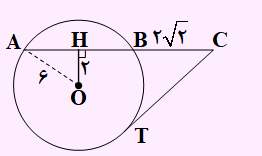
ابتدا در مثلث OAH، اندازه AH را طبق رابطه فیثاغورث به دست می آوریم. OH وتر را نصف خواهد کرد، لذا انداره HB و در نتیجه AB به دست خواهد آمد. حل طبق روابط طولی داریم:

به نمونه تست دوم در مورد روابط طولی در دایره توجه فرمایید:
تست) در شکل زیر مثلث ABC متساویالاضلاع است. با توجه به اندازههای دادهشده x کدام است؟

1- 4
2- 4.5
3- 5
4- 5.5
پاسخ : گزینه 3 پاسخ صحیح می باشد.
ابتدا فرض می کنیم اندازه سه ضلع مثلث متساوی الاضلاع برابر با a باشد. سپس رابطه طولی را برای نقطه B می نویسیم. از این طریق مقدار a به دست می آید. در نهایت رابطه طولی را برای نقطه C می نویسم تا مقدار x به دست آید. در واقع داریم:

برای مشاهده نمونه تست های بیشتر در مورد موضوع روابط طولی در دایره و نکات آن می توانید ویدئو آموزشی را مشاهده کنید.
سوالات متداول
اگر دو وتر دلخواه AB و CD در نقطه M داخل دایره متقاطع باشند، داریم:
MA×MB=MC×MD
اگر دو وتر دلخواه AB و CD در نقطه M خارج دایره متقاطع باشند، داریم:
MA×MB=MC×MD=MT2
MT مماس بر دایره در نقطه M است.





