در این فیلم آموزشی با موضوع حل تست های احتمال شرطی به کمک کاهش فضای نمونه ای آشنا خواهید شد.
فضای نمونه ای کاهش یافته در احتمال شرطی: در حالتی که فضای نمونه ای هم شانس است، شرطی کردن پیشامد A نسبت به پیشامد B مثل این است که فضای نمونه یعنی S را کنار گذاشته و B را فضای نمونه ای در نظر بگیریم. به عبارت دیگر قصد محاسبه احتمال پیشامد A را در فضای نمونه ای B داریم و اتفاقا احتمال روی فضای B نیز هم شانس است. در این حالت، B را فضای نمونه ای کاهش یافته می گوییم.
استراتژی حل مسائل : پیشامد B (شرط) را فضای نمونه ای در نظر گرفته و بدون استفاده از فرمول احتمال شرطی، مسئله را با قواعد احتمال ساده P(A)= n(A)/n(S) حل می کنیم.
با استفاده از استراتژی فضای نمونه ای کاهش یافته می توان برخی مسائلاحتمال شرطی را ساده تر حل نمود.
به نمونه تست اول توجه کنید:
تست اول) دو تاس را با هم پرتاب می کنیم. اگر تاس اول مضرب 3 باشد، با چه احتمالی مجموع دو تاس 7 می شود؟
الف) 1/3
ب) 1/6
ج) 1/12
د) 5/12
گزینه ب پاسخ صحیح می باشد.
چون گفته شده است تاس اول مضرب 3 است، بنابراین فضای نمونه ای به صورت زیر خواهد بود و کاهش می یابد.
B={(3,1),(3,2),(3,3),(3,4),(3,5),(3,6),(6,1),(6,2),(6,3),(6,4),(6,5),(6,6)}
مجموع(3,4) و (6,1) برابر 7 است. بنابراین برای محاسبه احتمال اینکه مجموع دو تاس 7 شود، داریم:
2/12= 1/6
به تست بعدی دقت کنید:
تست دوم) در یک خانواده سه فرزندی، می دانیم حداقل یک پسر وجود دارد. احتمال این که دو دختر داشته باشند، چقدر است؟
الف) 1/2
ب) 3/5
ج) 3/7
د) 3/8
گزینه ج پاسخ صحیح می باشد.
با توجه به اینکه می دانیم حداقل یک پسر وجود دارد، از اعضای فضای نمونه ای حالت (D, D , D)، یعنی اینکه سه دختر داشته باشند، حذف شده و فضای نمونه ای به صورت زیر کاهش می یابد:
B={(P,P,P),(P,P,D),(P,D,P),(P,D,D),(D,D,P),
(D,P,D),(D,P,P)}
سه حالت از حالات بالا دارای دو دختر است. بنابراین احتمال اینکه دو دختر داشته باشند به صورت زیر خواهد بود:
3/7
برای فهم بهتر موضوع به تست سوم دقت کنید:
تست سوم) تاسی را پرتاب می کنیم. اگر برآمد حاصل، مضرب 3 نباشد، احتمال اینکه 2 باشد، چقدر است؟
الف) 1/3
ب) 1/4
ج) 1/5
د) 1/6
گزینه ب پاسخ صحیح می باشد.
با توجه به اینکه برآمد حاصل، مضرب 3 نیست، فضای نمونه ای به صورت زیر کاهش می یابد:
B={1,2,4,5}
بنابراین احتمال اینکه عدد آمده 2 باشد در فضای نمونه ای بالا برابر با 1/4 خواهد شد.
به تست چهارم و پنجم توجه کنید:
تست چهارم) سکه ای را 4 بار پرتاب می کنیم، اگر بدانیم بار آخر پشت آمده است، احتمال اینکه دقیقا دو پشت در 4 پرتاب آمده باشد، کدام است؟
الف) 1/2
ب) 3/4
ج) 3/8
د) 3/16
گزینه ج پاسخ صحیح می باشد.
چون می دانیم بار آخر پشت آمده است، فضای نمونه ای دارای 2 ×2 ×2 ×1 یعنی 8 حالت می باشد. زیرا بار آخر تنها یک حالت پشت امکان پذیر است. ولی بقیه بارها دو حالت دارند.
با توجه به اینکه احتمال آمدن دقیقا دو پشت را خواسته، یک پشت که آمده است، از بین 3 پرتاب دیگر، باید یک پشت دیگر بیاید. یعنی داریم:
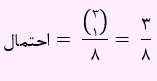
تست پنجم) در کیسه ای 2 کارت دو رو سبز، 3 کارت دو رو سفید و 4 کارت یک رو سبز و یک رو سفید موجود است. یکی از کارت ها را به تصادف برداشته و مشاهده می کنیم که یک روی آن سفید است. چقدر احتمال دارد روی دیگر آن نیز سفید باشد؟
الف) 3/7
ب) 3/5
ج) 7/9
د) 3/14
گزینه ب پاسخ صحیح می باشد.
با توجه به اینکه می دانیم یک روی کارت مشاهده شده سفید است، فضای نمونه ای دارای 3×2+4 یعنی 10 حالت می باشد. بنابراین احتمال خواسته شده به صورت زیر خواهد بود:
6/10= 3/5
برای آشنایی بیشتر با موضوع فضای نمونه ای کاهش یافته در احتمال شرطی و تست های آن می توانید ویدئو آموزشی را مشاهده کنید.
در حالتی که فضای نمونه ای هم شانس است، می توان مسائل و تست های احتمال شرطی را به کمک کاهش فضای نمونه ای حل نمود و از فرمولهای احتمال شرطی استفاده نکرد.
در مسائل احتمال شرطی، در حالتی که فضای نمونه ای هم شانس باشد، شرطی کردن پیشامد A نسبت به پیشامد B مثل این است که فضای نمونه یعنی S را کنار گذاشته و B را فضای نمونه ای در نظر بگیریم. در این صورت، به B فضای نمونه ای کاهش یافته گفته می شود.
خیر. در مسائل احتمال شرطی، در حالتی که فضای نمونه ای هم شانس است، نیاز به استفاده از فرمول احتمال شرطی نبوده و می توان مسائل را با قواعد احتمال ساده حل نمود.
موسسه آموزشی فرهنگی گزینه دو برگزارکننده آزمون آزمایشی ویژه داوطلبان آزمون سراسری و آزمون های استاندارد ارزشیابی پیشرفت تحصیلی در دوره اول متوسطه و پایه های دهم و یازدهم می باشد. گزینه دو به عنوان یک موسسه پیشرو در زمینه خدمات نوین آموزشی، نرم افزارهای گوناگونی را جهت بهبود فرآیند آموزش و سنجش برای دانش آموزان و مدارس ارائه می کند
