در این فیلم آموزشی با موضوع هرون، کاربرد تبدیلات هندسی (یافتن کوتاه ترین مسیر) و نکات تستی آن آشنا خواهید شد.
مسئله هرون
مسئله هرون: دو نقطۀ A و B در یک طرف خط d قرار دارند. برای یافتن نقطهای روی خط d که مجموع فاصلههای آن از A و B مینیمم باشد، باید بازتاب نقطۀ A را نسبت به خط d یافت و از آن به نقطۀ B وصل نمود. مطابق شکل MA+MB همواره کمترین مجموع فواصل است.

مسئله هرون یکی از مسائل معروف یافتن کوتاه ترین مسیر می باشد.
نمونه تست یافتن کوتاه ترین مسیر
به نمونه تست زیر دقت کنید:
تست) میخواهیم در یک مسیر از نقطۀ A به خط d1 و سپس به خط d2 و در نهایت به نقطۀ B عبور برویم. برای پیدا کردن کوتاهترین مسیر به چه تبدیلهایی نیاز داریم؟
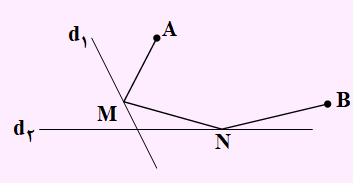
1- یک بازتاب
2- یک بازتاب و یک دوران
3- دو بازتاب
4- یک بازتاب و یک انتقال
پاسخ : گزینه 3 پاسخ صحیح می باشد.
در این مسئله از همان نکته هرون استفاده خواهیم کرد. ابتدا بازتاب A را نسبت به خط d1 پیدا می کنیم تا به نقطه ‘A برسیم. سپس نقطه ‘A را نسبت به خط d2 بازتاب داده تا به نقطه ”A برسیم. حال نقطه ”A را به B وصل خواهیم کرد. در اثر این برخورد نقطه N به دست می آید. حال اگر N را به ‘A وصل کنیم نقطه ای مانند M به دست خواهد آمد. یعنی مسیر AMNB در شکل زیر کوتاه ترین مسیر می باشد. مطابق شکل، به دو بازتاب نیاز داریم.

به تست دوم در مورد مسئله هرون توجه فرمایید:
تست) ABCD یک ذوزنقۀ قائمالزاویه است. اگر P نقطهای روی ساق قائم باشد که BP+PC کمترین مقدار خود را داشته باشد، اندازۀ PD کدام است؟

1- 2
2- 3
3- 3.5
4- 4
پاسخ : گزینه 4 پاسخ صحیح می باشد.
باید قرینۀ B را نسبت به AD یافته و آن را به نقطۀ C وصل کنیم. همانند شکل زیر

حال از تشابه به صورت زیر کمک می گیریم تا بتوانیم اندازه PD را به دست آوریم:

برای یادگیری بیشتر موضوع کاربرد تبدیلات هندسی در یافتن کوتاه ترین مسیر، مسئله هرون و نکات تستی آن می توانید فیلم آموزشی را مشاهده کنید.
سوالات متداول
یکی از کاربردهای بازتاب در هندسه در حل مسائل یافتن کوتاه ترین مسیر می باشد.
مسئله هرون مسئله ای است که در آن به دنبال یافتن کوتاه ترین مسیر بین دو نقطه می باشیم.





