در این فیلم آموزشی با موضوع انواع زوایا در دایره شامل زاویه مرکزی، زاویه محاطی، زاویه ظلّی و نکات تستی آن آشنا خواهید شد.
انواع زوایا در دایره
در دایره، هفت نوع زاویه وجود دارد:
1) زاویه مرکزی : راس این زاویه دقیقا مرکز دایره است و اضلاع آن شعاع های دایره می باشند. در شکل زیر زاویه O یک زاویه مرکزی است و اندازه زاویه مرکزی برابر با اندازه کمان رو به رو به زاویه می باشد.

2) زاویه محاطی : راس این زاویه روی محیط دایره است و اضلاع آن وترهای دایره می باشند. در شکل زیر زاویه α یک زاویه محاطی است و اندازه زاویه محاطی برابر با نصف اندازه کمان رو به رو به زاویه می باشد.

3) زاویه ظلّی : راس این زاویه روی محیط دایره است و یکی از اضلاع آن وتر دایره و ضلع دیگر آن مماس بر دایره می باشد. در شکل زیر زاویه α یک زاویه ظلّی است و اندازه زاویه ظلّی برابر با نصف اندازه کمان محصور در زاویه می باشد.

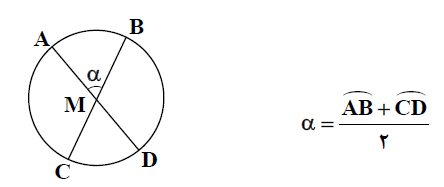
3) زاویه بین دو وتر : زاویه ای است که دو وتر متقاطع آن را تشکیل می دهند. در شکل زیر زاویه α یک زاویه بین دو وتر است و اندازه زاویه برابر با نصف مجموع اندازه کمان های رو به رو به زاویه می باشد.
5) زاویه بین دو قاطع : زاویه ای است که از دو وتری که بیرون همدیگر را قطع می کنند تشکیل شده است. در شکل زیر α زاویه بین دو قاطع است و اندازه آن برابر با نصف تفاضل کمان های بین دو زاویه می باشد.

6) زاویه بین قاطع و مماس : زاویه ای است که از دو وتری که بیرون همدیگر را قطع می کنند تشکیل شده است. در شکل زیر α زاویه بین قاطع و مماس است و اندازه آن برابر با نصف تفاضل کمان های بین دو زاویه می باشد.

7) زاویه بین دو مماس : زاویه ای است که از دو خط مماس بر دایره تشکیل شده است. در شکل زیر α زاویه بین دو مماس بوده و اندازه آن برابر با نصف تفاضل کمان های درونی و بیرونی می باشد.

دایره دارای هفت نوع زاویه می باشد.
نمونه تست انواع زاویا در دایره
به نمونه تست زیر دقت کنید:
تست) در شکل روبه رو داریم زاویه A=60° و B=35°. زاویۀ a چند درجه است؟

1- 60
2- 61
3- 62
4- 63
پاسخ : گزینه 1 پاسخ صحیح می باشد.
زوایای A و B، زاویه های محاطی هستند. بنابراین اندازه کمان های رو به روی آن دو را می توان با توجه به نکته به دست آورد. اندازه کمان BE با کم کردن 180 درجه از مکان BC به دست می آید. در نهایت زاویه α یک زاویه بین دو وتر متقاطع است که با توجه به نکته می توان اندازه آن را به دست آورد. در واقع داریم:

برای مشاهده نمونه تست های بیشتر در مورد موضوع انواع زوایا در دایره و نکات آن می توانید ویدئو آموزشی را مشاهده کنید.
سوالات متداول
زاویه مرکزی زاویه ای است که راس آن دقیقا مرکز دایره بوده و اضلاع آن شعاع های دایره می باشند. اندازه زاویه مرکزی برابر با اندازه کمان رو به رو به زاویه خواهد بود.
زایوه محاطی، زاویه ای است که راس آن روی محیط دایره قرار دارد و اضلاع آن وترهای دایره می باشند. اندازه زاویه محاطی برابر با نصف اندازه مکان رو به رو به زاویه خواهد بود.





