در این فیلم آموزشی در مورد توابع رادیکالی، دامنه و نمودار توابع رادیکالی توضیح داده شده است.
توابع رادیکالی، نمودار و دامنه آن
توابع رادیکالی: ساده ترین تابع رادیکالی، تابع با ضابطه f(x)=√x است. دامنه این تابع (∞+,Df=[0 است. شکل تابع رادیکالی به صورت زیر می باشد:

در دامنه توابع رادیکالی به دو نکته زیر باید دقت کرد:

در دامنه توابع رادیکالی به دو نکته زیر باید دقت کرد:
برای تعیین دامنه تابع رادیکالی با فرجه زوج باید عبارت زیر رادیکال را بزرگتر مساوی صفر قرار داد.
نمونه تست توابع رادیکالی
به نمونه تست های زیر توجه کنید:
تست: نمودار تابع f(x)=√x+1 -1 به کدام شکل است؟

گزینه 3 پاسخ صحیح می باشد.
نمودار تابع f(x)=√x+1 – 1 ، انتقال داده شده نمودار تابع y=√x است. برای رسم نمودار f(x)=√x+1 – 1 ، ابتدا نمودار y=√x را یک واحد به سمت چپ انتقال می دهیم. در مرحله بعد، نمودار به دست آمده را یک واحد به سمت پایین انتقال خواهیم داد تا نمودار f(x)=√x+1 – 1، به دست آید. همچنین باید دقت شود این تابع از نقطه (0 , 0) می گذرد. بنابراین گزینه 3 پاسخ صحیح می باشد.
به نمونه تست دوم توجه کنید:
تست: دامنه تابع زیر کدام است؟
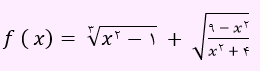
- [3, 3-]
- [1-, 3-]∩[∞+, 1]
- [1,R-[-1
- [2,R-[-2
گزینه 1 پاسخ صحیح می باشد.
به عنوان دامنه این تابع، باید عبارت زیر رادیکال با فرجه زوج را بزرگتر مساوی صفر قرار داد.
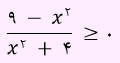
با توجه به اینکه مخرج این عبارت مثبت است، صورت را باید بزرگتر مساوی صفر قرار داد.
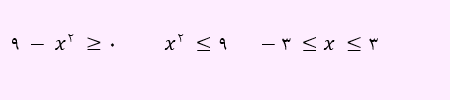
بنابراین دامنه تابع ذکر شده به دست آمد.
به منظور آشنایی بیشتر با موضوع توابع رادیکالی، نمودار و دامنه توابع رادیکالی ویدئو آموزشی را مشاهده کنید.
سوالات متداول
در دامنه توابع رادیکالی، اگر فرجه زوج باشد، باید عبارت زیر رادیکال را بزرگتر مساوی صفر قرار داد. اگر فرجه فرد بود، محدودیت مثبت منفی بودن عبارت زیر رادیکال را نخواهیم داشت.
در دامنه توابع رادیکالی با فرجه زوج، باید عبارت زیر رادیکال را بزرگتر مساوی صفر قرار داد.





