در این فیلم آموزشی با نمونه تست های اجتماع، اشتراک، تفاضل مجموعه ها و برابری مجموعه ها آشنا خواهید شد.
به نمونه تست اول دقت کنید:
تست اول) اگر A={a,b,c,d}، B={b,c,d,e} و داشته باشیم A∩B ⊆X ⊆A ∪B، چند مجموعه X وجود دارد؟
الف) 5
ب) 2
ج) 3
د) 4
گزینه 4 پاسخ صحیح می باشد.
با توجه به اینکه A∩B ⊆X ⊆A ∪B می باشد، داریم:
{b,c,d}⊆X ⊆{a,b,c,d,e}
با توجه به رابطه بالا، در مجموعه X، باید b,c,d قرار گیرد. ولی {a,e} می توانند باشند یا خیر. دو حالت برای وجود یا عدم وجود a و دو حالت برای بودن یا نبودن e وجود دارد. بنابراین در کل 2 ×2 یعنی 4 حالت داریم. بنابراین 4 مجموعه X وجود خواهد داشت.
به نمونه تست دوم دقت کنید:
تست دوم) اگر A مجموعه اعداد دو رقمی و B={5 k|k ∈A} آن گاه A ∩B چند زیر مجموعه دارد؟
الف) 256
ب) 512
ج) 1024
د) 2048
گزینه 3 پاسخ صحیح می باشد.
اعضای مجموعه A و B به صورت زیر می باشد:
A={10.11.12.13.….99}
B={50.55.60.65.70.75.80.85.90.95.100.…}
اشتراک دو مجموعه A و B شامل اعضای دو رقمی است . لذا تعداد آن ها برابر با 10 می باشد. یعنی داریم:
n ( A ∩B)=10 عضو
پس دارای 210 یعنی 1024 زیر مجموعه خواهد بود.
نمونه تست سوم در مورد تعداد زیر مجموعه می باشد:
تست سوم) اگر به ازای هر n ∈N داشته باشیم An={m∈Z |m ≥ -n ,2m ≤n}، آن گاه A3 ∩ A4 چند زیر مجموعه دارد؟
الف) 8
ب) 16
ج) 32
د) 64
گزینه ج پاسخ صحیح می باشد.
ابتدا A3 و A4 را به دست می آوریم:
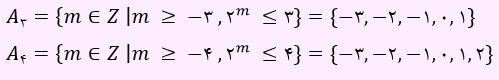
بنابراین A3 ∩ A4، برابر با {1, 0, 1- ,2- ,3-} خواهد شد که دارای 5 عضو است. بنابراین تعداد زیر مجموعه های آن مساوی با 25 یعنی 32 خواهد شد.
به منظور مشاهده نمونه تست های بیشتر در مورد موضوع اجتماع، اشتراک و تفاضل مجموعه ها فیلم آموزشی را مشاهده کنید.
فرض کنید A و B دو مجموعه دلخواه باشند، تفاضل دو مجموعه یعنی (A – B) شامل اعضایی است که به مجموعه A تعلق دارند ولی در B نیستند. در واقع داریم:
A-B={ x|x ∈A ∧x ∉B}
مؤسسه آموزشی فرهنگی گزینهدو برگزارکننده آزمون آزمایشی ویژۀ داوطلبان آزمون سراسری و آزمون‌های استاندارد ارزشیابی پیشرفت تحصیلی در دورۀ اول متوسطه و پایه‌های دهم و یازدهم می‌باشد. گزینهدو به‌عنوان یک مؤسسه پیشرو در زمینه خدمات نوین آموزشی، نرم‌افزارهای گوناگونی را جهت بهبود فرآیند آموزش و سنجش برای دانش‌آموزان و مدارس ارائه می‌کند.
مؤسسه آموزشی فرهنگی گزینهدو برگزارکننده آزمون آزمایشی ویژۀ داوطلبان آزمون سراسری و آزمون‌های استاندارد ارزشیابی پیشرفت تحصیلی در دورۀ اول متوسطه و پایه‌های دهم و یازدهم می‌باشد. گزینهدو به‌عنوان یک مؤسسه پیشرو در زمینه خدمات نوین آموزشی، نرم‌افزارهای گوناگونی را جهت بهبود فرآیند آموزش و سنجش برای دانش‌آموزان و مدارس ارائه می‌کند.
