در این فیلم آموزشی با موضوع تشابه چند ضلعی ها و نسبت اجزای متناظر آن آشنا خواهید شد.
تشابه چند ضلعی ها و نسبت اجزای متناظر
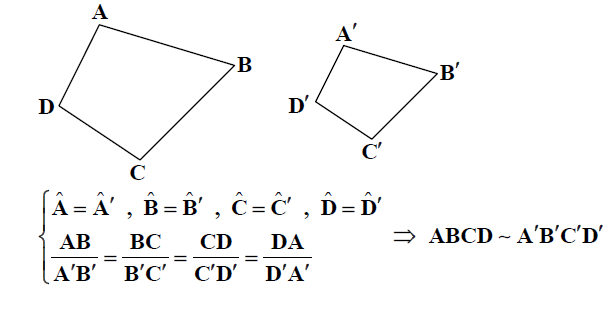
دو چندضلعی را متشابه گوییم هرگاه زاویه های آنها نظیر به نظیر مساوی و اضلاع متناظر آنها نیز متناسب باشند.
به طور مثال در شکل زیر، دو چهار ضلعی ABCD و ‘A’B’C’D متشابه هستند. زیرا هم زوایای آن ها نظیر به نظیر مساوی بوده و هم اضلاع متناظر آن ها نیز متناسب می باشد.
نکتۀ 1: دو nضلعی منتظم همواره متشابه اند.
نکتۀ 2: دو مستطیل با اضلاع متناسب و دو لوزی با زاویه های برابر، متشابه اند.
نکتۀ 3: نسبت محیط های دو چندضلعی متشابه با نسبت تشابه آنها برابر است و نسبت مساحت های آنها، مجذور نسبت تشابه می باشد.
دو n ضلعی منتظم همواره متشابه هستند.
نمونه تست تشابه دو چند ضلعی
به نمونه تست زیر دقت کنید:
تست: در شکل زیر، دو مستطیل ABCD و BCEF متشابه اند. اگر AB=1 و AD=3 باشد، مساحت ADEF چند برابر مساحت BCEF است؟

1- 4/3
2- 9/8
3- 10/9
4- 3/2
پاسخ : گزینه 3 پاسخ صحیح می باشد.
با توجه به اطلاعات داده شده در مسئله شکل به صورت زیر خواهد بود:

نسبت تشابه دو مستطیل را به صورت زیر می نویسیم:

حال، نسبت مساحت ADEF به BCEF را به صورت زیر به دست خواهیم آورد:

به منظور مشاهده نمونه تست های بیشتر در مورد موضوع تشابه چند ضلعی ها و نسبت اجزای متناظر می توانید به فیلم آموزشی مراجعه کنید.
سوالات متداول
دو چندضلعی زمانی متشابه هستند که زاویه های آنها نظیر به نظیر مساوی و اضلاع متناظر آنها نیز متناسب باشند.
نسبت مساحت های دو چند ضلعی متشابه برابر مجذور نسبت تشابه می باشد.





