در این فیلم آموزشی با موضوع همسایگی، همسایگی محذوف و همسایگی متقارن آشنا خواهید شد.
همسایگی چیست؟
در این فصل به سوالاتی از قبیل حد تابع در یک نقطه چیست و چه معنایی دارد، از آن چه استفاده ای می شود، پاسخ خواهیم داد. برای آنکه متوجه مفهوم حد شوید، نیاز است در ابتدا با مفهوم همسایگی آشنا شوید که در این فیلم آموزشی ابتدا به توضیح مفاهیم همسایگی می پردازیم. در فیلم های بعدی، مفهوم حد توضیح داده خواهد شد.
تعریف همسایگی: اگر x0 یک عدد حقیقی باشد، هر بازه باز شامل x0 است. اگر x0∈(a,b) آن گاه (a,b) یک همسایگی x0 است. در واقع x0 یک نقطه درونی از بازه است. به طور مثال (4, 1-) یک همسایگی 3، 2، صفر، و … است.
بازه (4, 1-) برای صفر همسایگی نمی باشد.
حال به حل یک نمونه تست درباره موضوع همسایگی خواهیم پرداخت.
تست) به فرض آنکه (2a-1, 6a+2) یک همسایگی 4 باشد. حدود a کدام است؟
- (2/5, 1/6)
- (6, 5/2)
- (5/2, 1/6)
- (6, 2/5)
گزینه 3 پاسخ صحیح می باشد.
برای آنکه (2a-1, 6a+2) ، همسایگی 4 باشد، باید 4 نقطه درونی از این بازه باشد. بنابراین روابط زیر را خواهیم داشت.
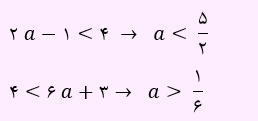
از دو رابطه بالا، نتیجه گرفته می شود، a باید بین 1/6 و 5/2 قرار گیرد. در حقیقت داریم a∈(1/6, 5/2) . بنابراین گزینه 3 پاسخ صحیح می باشد.
اگر x0∈(a,b) آن گاه (a,b) یک همسایگی x0 است.
همسایگی محذوف چیست؟
همسایگی محذوف: اگر بازه (a,b) همسایگی x0 باشد و x0 را از این همسایگی حذف کنیم. مجموعه (a,b)-x0 را همسایگی محذوف x0 می نامیم.
به طور مثال به {3}-(2,5) ، همسایگی محذوف x=3، گفته خواهد شد.
بازه (x0, x0+r) را همسایگی راست x0 و بازه (x0-r, x0) را همسایگی چپ x0 می نامیم.
نکته: نمایش های مختلف همسایگی محذوف x0 در حالات مختلف به صورت زیر است:

به منظور آشنایی بیشتر با موضوع همسایگی، همسایگی راست، چپ و همسایگی محذوف ویدئو آموزشی را مشاهده کنید.
سوالات متداول
اگر x0 یک عدد حقیقی باشد، هر بازه باز شامل x0 است. اگر x0 ϵ (a, b) آن گاه ( a, b) یک همسایگی x0 است. در واقع x0 یک نقطه درونی از بازه است.
اگر یک بازه مانند ( a, b) داشته باشیم که همسایگی x0 باشد. در صورتی که x0 را از این همسایگی حذف نمائیم، به مجموعه {x0}-(a,b) همسایگی محذوف x0 گفته خواهد شد.
به بازه ( x0, x0+r) همسایگی راست x0 و به بازه ( x0-r , x0) همسایگی چپ x0 گفته می شود.





