در این فیلم آموزشی با مباحث تابع جز صحیح، تابع پله ای و ویژگی های تابع جز صحیح آشنا خواهید شد.
تابع پله ای
تابعی را که بتوان دامنه آن ها را به تعدادی بازه تقسیم کرد به گونه ای که روی هر کدام از این بازه ها، ثابت باشد، تابع پله ای می گوییم. به عنوان مثال تابع زیر یک تابع پله ای می باشد. نمودار تابع مذکور نیز نشان داده شده است:

نمودار y=1/x در نواحی اول و سوم محور مختصات واقع می شود. چون xy=1 است، بنابراین x و y هم علامت هستند و به همین منظور نمودار این تابع در نواحی اول و سوم محور مختصات قرار خواهد گرفت. در واقع هر جایی x مثبت باشد، y نیز مثبت است و بالعکس. نمودار این تابع را در شکل زیر مشاهده می کنید:

تابع پله ای ، تابعی است که بتوان دامنه آن را به تعدادی بازه تقسیم کرد طوری که روی هر کدام از این بازه ها ثابت باشد.
توابع گنگ
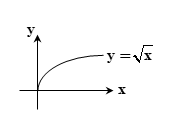
تابع y=√x یک تابع گنگ است. حال به بررسی چگونگی رسم نمودار و برد توابع گنگ می پردازیم. نمودار تابع مذکور را در زیر مشاهده می کید:
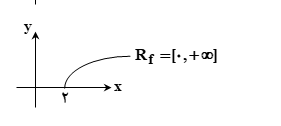
برای رسم نمودار y=√x-2 ، نیاز است نمودار y=√x را دو واحد به سمت راست انتقال دهیم. بنابراین برد این تابع از 0 تا مثبت بی نهایت یعنی به صورت Rf=[0, +∞] خواهد بود. نمودار این تابع در زیر نشان داده شده است
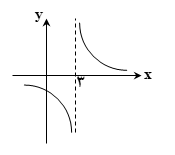
رسم نمودار y=x-3 را به خاطر داریم، بدین ترتیب برای رسم نمودار y=1/x-3 ، باید نمودار y=x-3 ، را سه واحد به سمت راست انتقال دهیم. برد این تابع برابر با Rf=R-{0} می باشد. نمودار تابع مذکور در زیر شکل زیر نشان داده شده است:
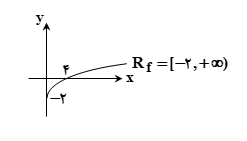
برای رسم نمودار y=√x – 2 ، نمودار y=√x را دو واحد به سمت پایین انتقال می دهیم. بنابراین برد این تابع از 2 – تا مثبت بی نهایت یعنی به صورت Rf=[-2, +∞] می باشد. به شکل زیر توجه کنید:
به منظور آشنایی بیشتر با توابع پله ای و جزء صحیح ویدئو آموزشی را مشاهده کنید.
سوالات متداول
تابع پله ای ، تابعی است که دامنه آن به تعدادی بازه تقسیم شده است به گونه ای که روی هر کدام از این بازه ها، تابع پله ای ثابت می باشد.
تابع جز صحیح تابعی است که به هر عدد حقیقی جز صحیح آن را نسبت دهد. تابع جز صحیح با نماد f(x)=[x] نشان داده می شود. در واقع تابع جز صحیح حالت خاصی از تابع پله ای می باشد.





