فصل دو حسابان یعنی تابع از فصول بسیار مهم می باشد که در کنکور سراسری نقش به سزایی دارد. در این ویدئو آموزشی با دامنه و برد تابع آشنا خواهید شد.
دامنه و برد تابع
اگر f یک تابع از مجموعه A به B باشد، آن گاه به هر عضو A دقیقا یک عضو از مجموعه B را نسبت می دهد. در این حالت : Df=A , Rf⊂B خواهد بود. یعنی دامنه تابع برابر با A و برد تابع، زیر مجموعه B می باشد.
حال در ادامه، به حل یک مثال خواهیم پرداخت.
مثال: دامنه تعریف تابع زیر را معلوم کنید.
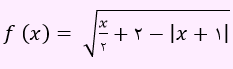
برای پیدا کردن دامنه تابع مذکور، باید عبارت زیر رادیکال را بزرگتر مساوی صفر قرار داد.
سپس عبارت داخل قدر مطلق دو حالت دارد یا بزرگتر مساوی صفر است یا کوچکتر مساوی صفر، دو حالت را در نظر خواهیم گرفت.
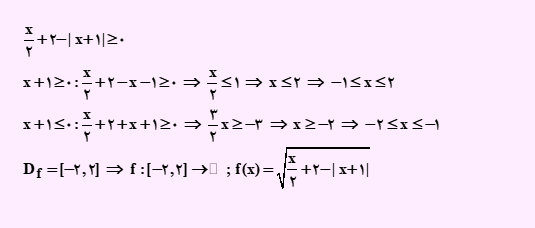
در نتیجه دامنه، اجتماع دو مجموعه بالا خواهد شد. بنابراین دامنه تابع Df=[-2,2] می باشد.
برای پیدا کردن دامنه تابعی که دارای عبارت رادیکالی است، باید عبارت زیر رادیکال را بزرگتر مساوی صفر قرار دارد.
به منظور آشنایی بیشتر با موضوع دامنه و برد تابع و نکات آن ویدئو آموزشی را مشاهده کنید.
سوالات متداول
اگر فرض کنیم، f یک تابع باشد در صورتی که f از مجموعه A به B باشد، در این حالت به هر عضو A دقیقا یک عضو از مجموعه B را نسبت می دهد. در این حالت دامنه تابع f برابر با A خواهدبود.
اگر فرض کنیم، f یک تابع باشد در صورتی که f از مجموعه A به B باشد، در این حالت به هر عضو A دقیقا یک عضو از مجموعه B را نسبت می دهد. در این حالت برد تابع، زیر مجموعه B خواهد بود.





