در این فیلم آموزشی به نکاتی در خصوص معادله درجه دوم و روابط بین آن خواهیم پرداخت.
نکات معادله درجه دوم
همان طور که آموختیم، در صورتی که بدانیم معادله درجه دوم دارای دو ریشه است، حاصل جمع و ضرب ریشه ها را از طریق ضرایب معادله درجه دوم می توان به دست آورد.
نکته: اگر S=α+β و P=αβ آنگاه مجموع عکس ریشه ها به صورت زیر خواهد بود:

نکته: هر عبارت متقارن بر حسب α و β را می شود بر حسب عبارتی بر حسب S و P نوشت. ( مجموع و ضرب ریشه ها)
عبارت متقارن بر حسب α و β یعنی اگر جای α و β را با یکدیگر تعویض نمائیم، عبارت تغییر نکند.
به طور مثال عبارت زیر چون متقارن است می توان آن را بر حسب ضرایب معادله نوشت.
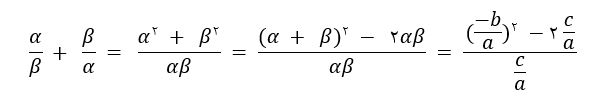
در معادله درجه دوم بدون دانستن ریشه ها، مجموع عکس ریشه ها را از طریق رابطه می توان به دست آورد.
مثال معادله درجه دوم
در این بخش برای درک بهتر نکات معادله درجه دوم به حل مثال خواهیم پرداخت.
مثال: اگر α و β ریشه های معادله x(1+2x)=2 باشند، مقدار عبارت زیر کدام است؟
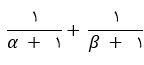
معادله به صورت 2x2+x-2=0 می باشد. بنابراین جمع ریشه ها مساوی 1/2- و ضرب ریشه ها برابر با 1- است. از جمع و ضرب ریشه ها در به دست آوردن حاصل عبارت به صورت زیر استفاده خواهیم کرد.
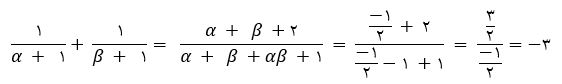
نکته: گاهی رابطه بین ریشه ها ظاهرا یک رابطه غیر متقارن است اما می توان آن را به رابطه متقارن تبدیل کرد و به کمک S و P آن را نوشت. (مجموع و ضرب ریشه ها)
مثال: در معادله 2x2-3x-4=0 ریشه ها α و β هستند. حاصل 2α2+3β را پیدا کنید؟
چون α ریشه است بنابراین در معادله صدق می کند. لذا رابطه زیر را خواهیم داشت.
2α2-3α-4=0 2α2=3α+4
بنابراین برای محاسبه حاصل 2α2+3β رابطه زیر را می نویسیم.
2α2+3β=3α+4+3β=3(α+Β)+4=3(1/5)+4=8/5
به منظور مشاهده نمونه تست های بیشتر در مورد معادله درجه دوم و روابط آن به ویدئو آموزشی مراجعه کنید.
سوالات متداول
بله. در صورتی که مطمئن باشیم معادله درجه دوم دارای دو ریشه است، جمع و ضرب ریشه ها را بدون دانستن خود ریشه ها از طریق ضرایب معادله درجه دوم می توان محاسبه کرد.
مجموع عکس ریشه ها بر حسب ضرایب برابر با منفی ضریب x تقسیم بر عدد ثابت معادله درجه دوم است.
در معادله درجه دوم، هر عبارت متقارن بر حسب α و β را بر حسب S و P می توان نوشت. ( مجموع و ضرب ریشه ها)
منظور از عبارت متقارن بر حسب α و β ، عبارتی است که اگر جای α و β را در آن با یکدیگر عوض کنیم، خود عبارت تغییری نکند.





