در این فیلم آموزشی به موضوع صفرهای تابع (ریشه های تابع) و نکات آن می پردازیم.
صفرهای تابع (ریشه های تابع) چیست؟
صفرهای تابع f مقادیری از دامنه تعریف تابع f هستند که f(x) به ازای آن ها صفر شود. در واقع صفرهای تابع طول نقاط تلاقی نمودار f با محور طول ها می باشند.
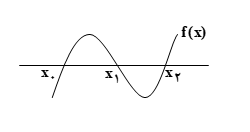
به طور مثال اگر داشته باشیم،f(x1)=f(x0)=f(x2)=0 ، آن گاه صفرها یا ریشه های تابع نقاط x0, x1, x2 خواهند بود.
نکته: اگر سهمی f(x)=ax2+bx+c=0 در دو نقطه به طول های α و β محور طول ها را قطع کند، آنگاه ، f(x)=a(x-α)(x-β) ضابطه آن خواهد بود. ( α و β صفرهای سهمی هستند)
نکته: سهمی اگر ماکزیمم داشته باشد و دهانه سهمی رو به پایین باشد، در این صورت در رابطه f(x)=a(x-α)(x-β) ، مقدار a<0 و منفی می باشد. اگر سهمی مینیمم داشته باشد و دهانه سهمی رو به بالا باشد، در آن صورت، a>0 و مثبت خواهد بود.
صفرهای تابع، مقادیری از دامنه تعریف تابع f هستند که تابع به ازای آن ها صفر شود.
مثالی از صفرهای تابع
در این بخش به حل یک مثال در رابطه با صفرهای تابع (ریشه های تابع) می پردازیم.
مثال: اگر سهمی f(x)=ax2+bx+c در دو نقطه به طول های 1- و 5 محور طول ها را قطع کند و دهانه سهمی رو به پایین باشد. همچنین نقطه تلاقی سهمی با محور عرض ها نقطه 2 باشد، ضابطه آن را بنویسید؟
در این سهمی دو ریشه را داده است، بنابراین طبق رابطه ضابطه را می نویسیم.
f(x)=a(x-α)(x-β) ، طبق این ضابطه سهمی به صورت زیر می باشد. چون دهانه سهمی رو به پایین است پس ضریب a منفی خواهد بود.
y=a(x-5)(x+1)
از طرفی نقطه تلاقی سهمی با محور عرض ها نقطه 2 است. لذا y(0)=2 می باشد. بنابراین y(0)=2 ، را در ضابطه قرار می دهیم و ضریب a را به دست می آوریم. در این صورت ضریب a برابر با 2/5- خواهد شد.
به منظور یادگیری نمونه تست های بیشتر از موضوع صفرهای تابع (ریشه های تابع) و نکات آن ویدئو آموزشی را مشاهده کنید.
سوالات متداول
منظور از صفرهای تابع، ریشه های تابع می باشند. صفر تابع، نقطه ای از دامنه تعریف تابع است که تابع در آن نقطه با محور طول ها تلاقی داشته باشد.
سهمی اگر ماکزیمم داشته باشد و دهانه سهمی رو به پایین باشد، a<0 و منفی می باشد.
اگر سهمی مینیمم داشته باشد و دهانه سهمی رو به بالا باشد، در آن صورت، a>0 و مثبت خواهد بود.
عالی