فاصله نقطه از خط جز مباحثی است که در کنکور سراسری بسیار پر کاربرد می باشد. در این فیلم آموزشی به موضوع فاصله نقطه از خط، فاصله دو خط موازی و یافتن قرینه نقطه نسبت به خطوط خاص و نقطه خواهیم پرداخت.
فاصله نقطه از خط
فرض کنید معادله خط به صورت ax+by+c=0 باشد. در این صورت فاصله نقطه A(x0,y0) تا خط مذکور از طریق رابطه زیر محاسبه می شود:

حال به بررسی حالات خاص می پردازیم.
اگر خط عمودی بوده و به شکل x=k باشد، آن گاه فاصله برابر با اختلاف x های نقطه و معادله خط خواهد بود. در واقع در این حالت فاصله از طریق رابطه |d=|k-x0 محاسبه می شود.
اگر خط افقی بوده و به صورت y=k باشد، آن گاه فاصله برابر با اختلاف y های نقطه و معادله خط خواهد بود. در حقیقت در این حالت فاصله از طریق رابطه |d=|k-y0 محاسبه خواهد شد.
تست) دو نقطه روی خط y=x-1 قرار دارند که فاصله آن ها از خط 2x-2y=5 برابر 13√ است. مجموع طول این دو نقطه چه عددی است؟
- 6-
- 4-
- 4
- 2
گزینه دو پاسخ صحیح می باشد.
ابتدا یک نقطه شناور A(α, α-1) را روی خط y=x-1 در نظر می گیریم. حال فاصله نقطه A را تا خط 2x-2y-5=0 از طریق رابطه زیر به دست می آوریم و برابر با 13√ قرار می دهیم.
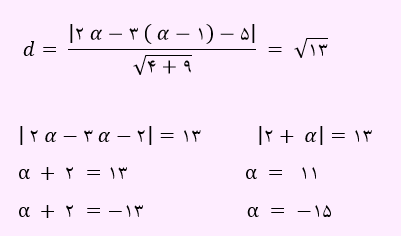
بنابراین مجموع طول این دو نقطه برابر با 4- خواهد بود. لذا گزینه دو پاسخ صحیح می باشد.
فاصله دو خط موازی از یکدیگر
فاصله دو خط موازی به معادله خط ax+by+c=0 و ax+by+c’=0 از طریق رابطه زیر به دست می آید:
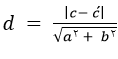
اگر دو ضلع مقابل یک مربع با مساحت 5 روی خطوط 2x+4y+3=0 و ax-6y+b=0 باشند، مقدار کدام میتواند باشد؟
- 7/5
- 9/5
- 22/5
- 15/5
گزینه یک پاسخ صحیح می باشد.
راه حل این مسئله به صورت زیر است:
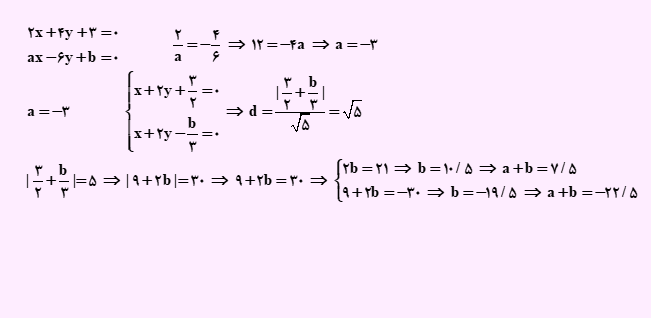
فاصله نقطه از خط عمودی برابر با اختلاف x های نقطه و معادله خط می باشد.
قرینه نقطه
اگر A(α, β) ، نقطه ای دلخواه در صفحه باشد، آنگاه روابط زیر را خواهیم داشت.

به منظور یادگیری بیشتر در مورد موضوع فاصله نقطه از خط، فاصله دو خط موازی از یکدیگر و نکات آن ویدئو آموزشی را مشاهده کنید.
سوالات متداول
اگر خط مورد نظر عمودی بوده و به شکل x=k باشد، آن گاه فاصله نقطه مذکور تا خط مورد نظر برابر با اختلاف x های نقطه و معادله خط خواهد بود.
اگر خط مورد نظر افقی بوده و به صورت y=k باشد، آن گاه فاصله نقطه مذکور تا خط مورد نظر برابر با اختلاف y های نقطه و معادله خط خواهد بود.
فرض کنیم نقطه مورد نظر A (α .β) ، نقطه دلخواهی در صفحه باشد. در این صورت قرینه A نسبت به نقطه دلخواهی مانند O ( x0 .y0)، نقطه A1 (2x0– α .2y0– β) خواهد بود.





