در این فیلم آموزشی با موضوع قضیه سینوس ها در هندسه و نکات مهم کنکوری آن آشنا خواهید شد.
قضیه سینوس ها
در مثلث ABC با اندازه های اضلاع a، b و c، نسبت اندازۀ هر ضلع به سینوس زاویۀ مقابل، همواره ثابت و برابر قطر دایرۀ محیطی است.

قضیه سینوس ها نسبت اندازه هر ضلع به سینوس زاویه مقابل را نشان می دهد.
نمونه تست قضیه سینوس ها
به نمونه تست زیر دقت کنید:
تست: در مثلث ABC، اندازه زاویه A=120° ، B=15° و AB=√6 است. اندازۀ ضلع BC کدام است؟
1- 3
2- 6√2
3- 4
4- 2√3
پاسخ : گزینه 1 پاسخ صحیح می باشد.
با توجه به اندازه زوایای داده شده در صورت سوال اندازه زاویه C در شکل زیر برابر با °45 خواهد بود.
C=180°-120°-15°=45°

حال قضیه سینوس ها را در مثلث ABC نوشته تا اندازه ضلع BC به دست آید:

به تست دوم در مورد موضوع قضیه سینوس ها توجه فرمایید:
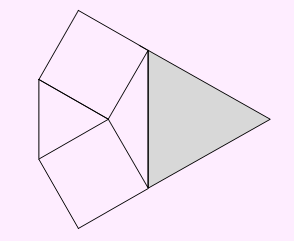
تست (سراسری 93): در یک مثلث متساوی الاضلاع بر روی دو ضلع آن، دو مربع بنا شده است. مساحت مثلث سایه زده، چند برابر مساحت مثلث اصلی است؟
1- 2
2- 2.25
3- 3
4- 4
پاسخ : گزینه 3 پاسخ صحیح می باشد.
مثلث اولیه چون متساوی الاضلاع است تمام زاویای آن 60 درجه می باشد. از طرفی زوایای تمام مربع ها برابر با 90 درجه خواهد بود. با توجه به اندازه های داده شده در صورت سوال اندازه مابقی زوایای داده نشده به صورت شکل زیر خواهد بود:

حال از قضیه سینوس ها به صورت زیر کمک می گیریم تا بتوانیم نسبت مساحت دو مثلث را به دست آوریم:
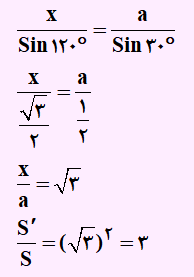
به منظور مشاهده نمونه تست های بیشتر در مورد قضیه سینوس ها و نکات آن می توانید به فیلم آموزشی مراجعه کنید.
سوالات متداول
قضیه سینوس ها بیان می کند اندازه هر ضلع به سینوس زاویه مقابل همواره ثابت بوده و برابر با قطر دایره محیطی می باشد.
طبق قضیه سینوس ها اندازه هر ضلع به سینوس زاویه مقابل همواره ثابت بوده و برابر با قطر دایره خواهد بود.





