در این فیلم آموزشی به حل نمونه تست هایی در مورد موضوع ترکیب توابع و تابع معکوس می پردازیم.
نمونه تست
در ابتدا به حل نمونه تست اول در مورد ترکیب دو تابع می پردازیم:
تست1) اگر f={(1,3), (22), (3,1), (4,0)} و g={(2,1), (3,3), (0,2)}. برد تابع g-1of کدام است؟
- {3, 2, 0}
- {4, 3, 2, 1}
- {3, 2, 1}
- {3, 4, 0}
گزینه 1 پاسخ صحیح می باشد.
ابتدا g-1 را با تعویض زوج مرتب های آن به صورت زیر پیدا می کنیم.
g-1={(1,2), (3,3), (2,0)}
تابع g-1of به صورت زیر خواهد بود.
g-1of={(1,3), (2,0), (3,2)}
بنابراین دامنه و برد تابع g-1of به شکل زیر می باشد.
Dg-1of={1, 2, 3} Rg-1of={0, 2, 3}
لذا گزینه 1 پاسخ صحیح خواهد بود.
نکته: با داشتن ضابطه f و g می توانیم ضابطه fog و gof را بیابیم. گاهی اوقات یکی از دو ضابطه fog و gof را می دهند و باید ضابطه تابع را به دست آوریم. به عنوان نمونه، به تست های زیر توجه کنید.
تست2) اگر f(x)=x+1/x-1 و g(x)=x2+2/x2+1 ، مقدار چه عددی است؟
- 2
- 3
- 4
- 5
گزینه 4 پاسخ صحیح می باشد.
مقدار g(1) از طریق رابطه زیر به دست خواهد آمد.
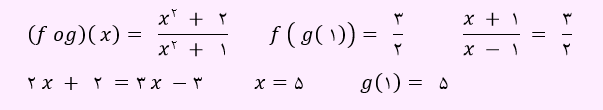
بنابراین مقدار g(1) برابر با 5 خواهد شد. لذا گزینه 4 پاسخ صحیح می باشد.
در این بخش به حل نمونه تست بعدی در مورد ترکیب توابع می پردازیم:
تست 3 ) اگر g(x)=x-√x و نمودار تابع f( x) محور x ها را در 2 نقطه A و B به طول 6 و 1/4- قطع کند، آن گاه نمودار f o g ( x) محور x ها را با کدام طول قطع می کند؟
- 4 و 1/9
- 1/4و 9
- 1/4 و 4
- 4و 9
گزینه 2 پاسخ صحیح می باشد.
وقتی نمودار تابع f( x) محور x ها را در 2 نقطه A و B به طول 6 و 1/4- قطع کند، یعنی به ازای x = 6 و x =-1/4 تابع f (x)، صفر خواهد شد. بنابراین می توان روابط زیر را نوشت.
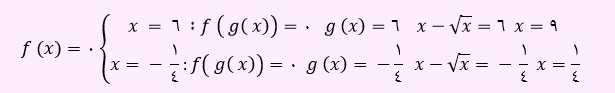
لذا گزینه 2 پاسخ صحیح می باشد.
برای مشاهده نمونه تست های بیشتر در مورد موضوع ترکیب توابع و تابع معکوس به فیلم آموزشی رجوع کنید.
سوالات متداول
بله این امر امکان پذیر است. به عنوان مثال با در اختیار داشتن ضابطه f و gof می توانیم ضابطه g را به دست آوریم.
برای به دست آوردن معکوس تابع دارای اعضای زوج مرتب، باید جای اعضای زوج مرتب را با یکدیگر تعویض نمائیم.
خیر تمام توابع معکوس پذیر نیستند. شرط لازم و کافی برای اینکه تابع معکوس پذیر باشد، این است که تابع یک به یک باشد.





