در این فیلم آموزشی، واحدی برای اندازه گیری زاویه به نام رادیان را معرفی خواهیم نمود. همچنین به مفاهیم نسبت های مثلثاتی برای برخی از زوایای خاص، اتحادهای مثلثانی در فصل سوم حسابان پرداخته شده است.
اندازه گیری زاویه بر حسب رادیان
درجه یکی از واحدها برای اندازه گیری زاویه است که در سال دهم در کتاب ریاضی با آن آشنا شدیم.
رادیان واحدی برای اندازه گیری زاویه است. به طور مثال اگر یک زاویه 60 درجه باشد، برابر با π/3 رادیان است. درجه و رادیان با یکدیگر رابطه زیر را خواهند داشت.
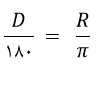
در رابطه بالا، D بر حسب درجه و R بر حسب رادیان می باشد.
مثال) اگر یک زاویه 30 درجه باشد، چند رادیان است؟
طبق رابطه بیان شده می توان از طریق معادله زیر، زاویه را برحسب رادیان حساب نمود.
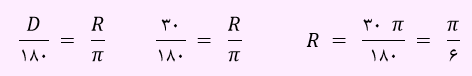
بنابراین بر طبق رابطه بالا 30 درجه معادل با π/6 رادیان است.
به مثال دوم توجه کنید:
مثال) π/4 چند درجه است؟
طبق رابطه بیان شده می توان به صورت زیر، زاویه را بر حسب درجه حساب نمود.
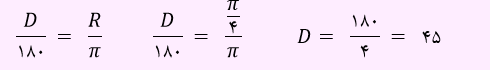
بنابراین Π/4 برابر با 45 درجه می باشد.
یا می توان در راه حلی راحت تر به جای Π عدد 180 را قرار داد.
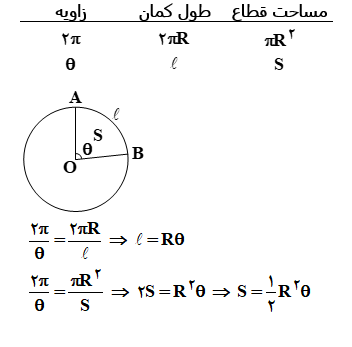
نکته: اگر زاویه یک دور کامل در دایره باشد، (2π) باشد و شعاع برابر R باشد، آن گاه اندازه طول کمان یعنی محیط دایره مساوی 2πR خواهد شد. مساحت کل دایره πR2 می شود.
اگر زاویه را θ ، انتخاب کنیم، طول کمان l و S مساحت باشد، رابطه بین S,l,θ به صورت زیر خواهد بود.
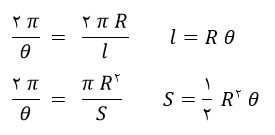
به شکل زیر دقت کنید:
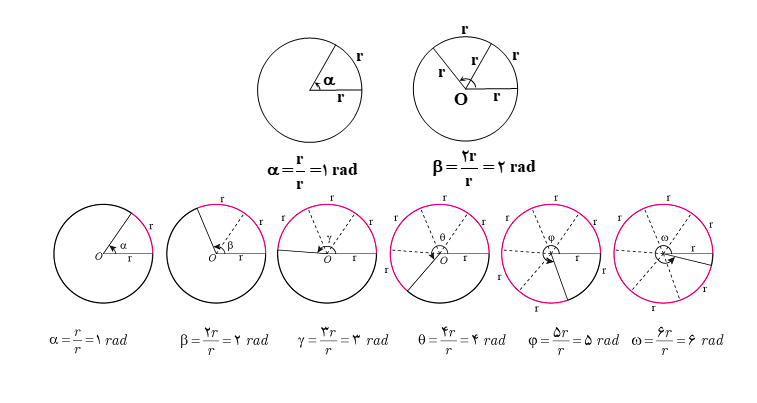
در هر دایره دلخواه، اندازه زاویه مرکزی که طول کمان رو به رو به آن، برابر طول شعاع دایره باشد یک رادیان است. هر رادیان تقریبا 57 درجه است. به شکل زیر توجه کنید:
به منظور آشنایی بیشتر با موضع اندازه گیری زاویه بر حسب رادیان و نمونه تست های آن ویدئو آموزشی را مشاهده کنید.
سوالات متداول
رادیان واحدی است که به منظور اندازه گیری زاویه از آن استفاده خواهد شد. در هر دایره دلخواه، اندازه زاویه مرکزی که طول کمان رو به رو به آن، مساوی طول شعاع دایره باشد یک رادیان است.
رادیان و درجه دو واحد در مثلثات هستند که به منظور اندازه گیری زاویه از آن ها استفاده می شود.





