در این فیلم آموزشی به موضوع یافتن معادله درجه دوم با داشتن ریشه های آن خواهیم پرداخت.
اگر بخواهیم معادله درجه دوم تشکیل دهیم که ریشه های آن ها دو عدد معلوم α و β باشند، با فرض S=α+β و P=αβ آنگاه معادله مورد نظر به صورت x2-Sx+P=0 خواهد بود. حال در ادامه برای فهم بیشتر به حل چند نمونه مثال خواهیم پرداخت.
مثال: معادله درجه دوم با ریشه های 1- و 4 را بیابید؟
در آن صورت S=3 و P=-4 خواهد شد. بنابراین معادله درجه دوم طبق رابطه x2-Sx+P=0 ، برابر با x2-3x-4=0 می شود.
در صورت داشتن ریشه ها، می توان معادله درجه دوم را نوشت.
در این قسمت به حل یک نمونه تست درباره معادله درجه دوم که مشابه آن در تست های کنکور سراسری بسیار دیده شده است، خواهیم پرداخت.
تست: اگر α و β ریشه های 2x2-x-2=0 باشند، معادله درجه دومی که ریشه های آن β/2α و α/2β باشد، کدام است؟
گزینه 4 پاسخ صحیح می باشد.
در معادله ذکر شده چون Δ>0 است، بنابراین معادله دارای دو ریشه متمایز α و β می باشد.
در صورت سوال معادله درجه دومی خواسته که ریشه های آن معلوم است. بنابراین نیاز است S و P آن ها را بیابیم و سپس معادله را بنویسیم. پس P و S را به دست می آوریم.
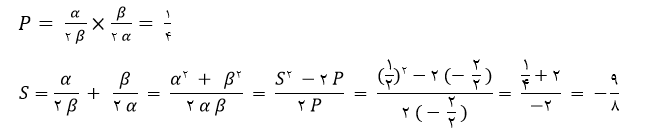
لذا با توجه به S و P، معادله درجه دوم به صورت زیر خواهد شد.
طرفین را در هشت ضرب می کنیم و معادله به شکل 8x2+9x+2=0 می شود.
بنابراین گزینه 4 پاسخ صحیح است.
به منظور مشاهده نمونه تست های بیشتر در مورد نوشتن معادله درجه دوم با داشتن ریشه ها می توانید ویدئو آموزشی را مشاهده کنید.
بدین منظور نیاز است، در آغاز حاصل جمع و حاصل ضرب ریشه ها را بیابیم و سپس از طریق آن معادله مربوطه را بنویسیم.
در معادله درجه دوم در صورتی که Δ مثبت باشد، معادله دارای دو ریشه متمایز خواهد بود
در معادله درجه دوم در صورتی که Δ منفی باشد، معادله ریشه ندارد.
مؤسسه آموزشی فرهنگی گزینهدو برگزارکننده آزمون آزمایشی ویژۀ داوطلبان آزمون سراسری و آزمون‌های استاندارد ارزشیابی پیشرفت تحصیلی در دورۀ اول متوسطه و پایه‌های دهم و یازدهم می‌باشد. گزینهدو به‌عنوان یک مؤسسه پیشرو در زمینه خدمات نوین آموزشی، نرم‌افزارهای گوناگونی را جهت بهبود فرآیند آموزش و سنجش برای دانش‌آموزان و مدارس ارائه می‌کند.
مؤسسه آموزشی فرهنگی گزینهدو برگزارکننده آزمون آزمایشی ویژۀ داوطلبان آزمون سراسری و آزمون‌های استاندارد ارزشیابی پیشرفت تحصیلی در دورۀ اول متوسطه و پایه‌های دهم و یازدهم می‌باشد. گزینهدو به‌عنوان یک مؤسسه پیشرو در زمینه خدمات نوین آموزشی، نرم‌افزارهای گوناگونی را جهت بهبود فرآیند آموزش و سنجش برای دانش‌آموزان و مدارس ارائه می‌کند.
