در این فیلم آموزشی به موضوع نسبت های مثلثاتی برخی از زوایای خاص خواهیم پرداخت.
زوایای خاص
در ابتدا با زوایای خاص و پس از آن با نسبت های مثلثاتی آن ها آشنا خواهیم شد.
زوایای خاص به چه چیزی گفته می شود؟
اگر θ ، مشخص باشد، به زوایای زیر، زوایای خاص گفته خواهد شد.
اگر زاویه قرینه شود، کسینوس تغییر علامت نمی دهد، ولی سه نسبت دیگر یعنی سینوس، تانژانت و کتانژانت قرینه خواهند شد. در حقیقت می توان بدین منظور روابط زیر را نوشت:
لازم به ذکر است ضرب تانژانت و کتانژانت در یکدیگر برابر با یک است. همچنین تانژانت یک زاویه، از تقسیم سینوس بر کسینوس و کتانژانت یک زاویه از تقسیم کسینوس بر سینوس به دست خواهد آمد.

نسبت های مثلثاتی زوایای متمم و مکمل
نکته : هر موقع π/2 ، در میان رابطه بین زوایا داشتیم، نسبت ها عوض خواهد شد. یعنی سینوس به کسینوس، کسینوس به سینوس، تانژانت به کتانژانت و کتانژانت به تانژانت تبدیل خواهد شد.
بنابراین برای نسبت های مثلثاتی بین زاویای متمم، روابط زیر را خواهیم داشت.

نکته: اگر θ ، زاویه ای حاده باشد، π/2-θ ، در ناحیه اول است و در ناحیه اول نسبت ها همگی مثبت هستند.
اگر θ ، زاویه ای حاده باشد، Π-θ ، در ناحیه دوم است. در ناحیه دوم سینوس مثبت، کسینوس منفی، تانژانت و کتانژانت منفی خواهد بود.
بنابراین برای زوایای مکمل روابط زیر را خواهیم داشت.

اگر θ ، زاویه ای حاده باشد، π+θ ، در ناحیه سوم قرار دارد. در ناحیه سوم سینوس و کسینوس منفی، تانژانت و کتانژانت مثبت می باشد. لذا روابط زیر را داریم.
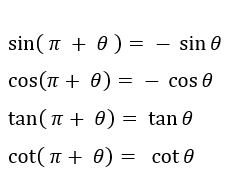
در واقع، در روابط بالا نسبت عوض نشد و علامت در ناحیه سوم ملاحظه شد.
برای π/2+θ ، نسبت های مثلثاتی زیر را خواهیم داشت. چون ، π/2 داریم، نسبت ها عوض خواهد شد. همچنین به علت اینکه در ناحیه دوم قرار می گیرد، سینوس مثبت، کسینوس منفی، تانژانت و کتانژانت منفی خواهد شد.
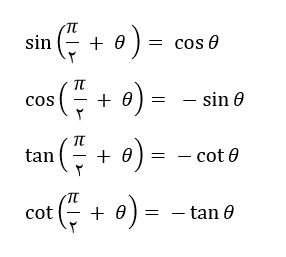
حاصل ضرب تانژانت و کتانژانت یک زاویه در یکدیگر برابر با یک می باشد.
به منظور آشنایی بیشتر با نمونه تست های مساحت جانبی مخروط و نکات آن فیلم آموزشی را مشاهده کنید.
سوالات متداول
در این قسمت سینوس زاویه π/2-θ ، را می خواهیم. چون π/2 داریم، نسبت ها عوض خواهند شد. π/2-θ، در ناحیه اول قرار می گیرد و در این ناحیه سینوس مثبت است. در واقع سینوس متمم زاویه θ برابر با cosθ خواهد شد.
حاصل ضرب تانژانت و کتانژانت در یکدیگر، یک خواهد شد.
تانژانت یک زاویه برابر است با تقسیم سینوس بر کسینوس و کتانژانت یک زاویه مساوی است با تقسیم کسینوس بر سینوس.





