در این فیلم آموزشی مبحث خط، نوشتن معادله خط و محاسبه شیب خط توضیح داده شده است.
نوشتن معادله خط
خط در صفحه یک منحنی از درجه اول است. معادله خط به صورت y=ax+b می تواند باشد که به a، شیب خط و به b عرض از مبدا گفته خواهد شد. خط با جهت مثبت محور x ها زاویه ای مانند α می سازد. به tan(α) ، شیب خط گفته خواهد شد. به فاصله نقطه ای که خط در آن محور عرض ها را قطع می کند تا مبدا، عرض از مبدا گفته می شود. همچنین به فاصله نقطه ای که خط در آن محور طول ها را قطع می کند تا مبدا، طول از مبدا گفته خواهد شد. همچنین معادله خط به صورت ax+by+c=0 نیز می تواند باشد.
در معادله خط ax+by+c=0 ، اگر x را برابر صفر قرار دهیم، آن گاه عرض از مبدا برابر با y=-c/b و اگر y را برابر صفر قرار دهیم، آن گاه طول از مبدا برابر با x=-c/a خواهد شد.
معادله خط در حالات خاص
حال به بررسی معادله خط در حالات خاص می پردازیم.
- اگر خط افقی باشد، معادله خط به صورت y = k می باشد.
- اگر خط عمودی باشد، معادله خط به صورت x = k خواهد بود.
- معادله خطی که از مبدا بگذرد به صورت y = ax است.
- اگر خطی محور x ها را در نقطه a و محور y ها را در نقطه b قطع کند، آن گاه معادله خط آن به صورت زیر خواهد بود.
در شکل زیر معادله خط در حالت های خاص نشان داده شده است:

در معادله خط y=ax+b، به a شیب خط و به b عرض از مبدا گفته خواهد شد.
محاسبه شیب خط
شیب معادله خطی که از دو نقطه معلوم و بگذرد با تقسیم تفاضل عرض ها بر تفاضل طول ها به دست خواهد آمد. در واقع برای محاسبه شیب خط معادله مذکور رابطه زیر را خواهیم داشت.

آن گاه با داشتن یک نقطه و شیب خط می توان معادله خط را به راحتی به صورت زیر نوشت.

تست: عمود منصف دو نقطه A(-1,4) و B(3,2) نیمساز ناحیۀ دوم و چهارم را با کدام طول قطع میکند؟
- 1/3
- 3
- 1/3
- 3-
گزینه 3 پاسخ صحیح می باشد.
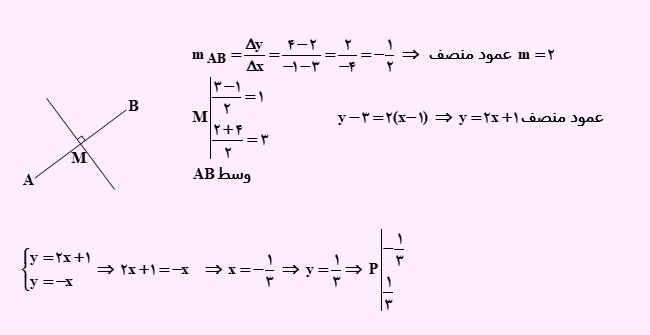
به منظور مشاهده نمونه تست های بیشتر در مورد موضوع معادله خط و محاسبه شیب خط می توانید به ویدئو آموزشی مراجعه کنید.
سوالات متداول
معادله خطی که از مبدا می گذرد، برابر با y=ax می باشد.
اگر دو نقطه معلوم داشته باشیم، شیب خطی که از دو نقطه معلوم بگذرد برابر است با تقسیم تفاضل عرض ها بر تفاضل طول ها.
فاصله دو نقطه در صفحه از یکدیگر برابر است با جذر مجموع تفاضل عرضها به توان دو و تفاضل طول ها به توان دو.






عالی