در این فیلم آموزشی با موضوع حالت های تشابه دو مثلث، حالت تساوی دو زاویه، حالت تناسب سه ضلع، حالت تساوی یک زاویه و تناسب اضلاع آن دو زاویه و تست های آن آشنا خواهید شد.
حالت های تشابه دو مثلث
حالت های تشابه دو مثلث شامل موارد زیر است:
1) حالت تساوی دو زاویه
2) حالت تناسب سه ضلع
3) حالت تساوی یک زاویه و تناسب اضلاع آن دو زاویه
حالت تساوی دو زاویه، پرکاربردترین حالت تشابه دو مثلث می باشد.
نمونه تست حالت های تشابه دو مثلث
به نمونه تست زیر دقت کنید:
تست: در شکل زیر دو ارتفاع BH و CK رسم شده اند. کدام مثلث با بقیۀ مثلث ها در گزینه ها لزوماً متشابه نیست؟

1- OHC
2- OBK
3- ACK
4- BHC
پاسخ : گزینه 4 پاسخ صحیح می باشد.
دو مثلث OHC و OBK دو زاویه برابر قائم دارند. همچنین زاویای متقابل به راس آن ها نیز با یکدیگر مساوی می باشند. لذا این دو مثلث بنا بر حالت تساوی دو زاویه متشابه هستند. همچنین دو مثلث ACK و OHC بنا بر حالت تساوی دو زاویه متشابه می باشند. زیرا زاویه c در هر دو این مثلث ها یکسان است و همینطور هر دو مثلث دارای زاویه قائمه هستند.
بنابراین سه مثلث OHC، OBK و ACK به حالت تساوی دو زاویه متشابه اند و تنها مثلث BHC با این مثلث ها متشابه نمی باشد.
به نمونه تست دوم در مورد حالت های تشابه دو مثلث توجه فرمایید:
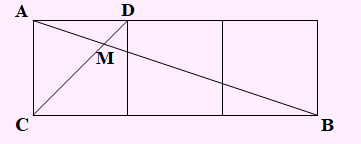
تست: در شکل زیر سه مربع به ضلع واحد، کنار هم قرار دارند. فاصلۀ MA چند برابر 10√ است؟
1- 1/3
2- 1/4
3- 2/9
4- 1/5
پاسخ : گزینه 2 پاسخ صحیح می باشد.
با توجه به روابط داده شده در صورت سوال، شکل به صورت زیر خواهد بود:

دو خط موازی هستند، لذا باعث ایجاد زاویه های برابر می شوند. در واقع دو زاویه A1 و B1 مساوی هستند. همچنین دو زاویه C1 و D1 نیز مساوی می باشند. بنابراین دو مثلث AMD و MBC به حالت تساوی دو زاویه متشابه می شوند. لذا نسبت اضلاع را می نویسم. بنابراین داریم:

در نهایت اندازه ضلع AB براساس قضیه فیثاغورث برابر با 10√ به دست می آید. بنابراین فاصله MA، برابر 1/4 عدد 10√ می باشد.
برای یادگیری نکات بیشتری در مورد موضوع حالت های تشابه دو مثلث می توانید ویدئو آموزشی را مشاهده کنید.
سوالات متداول
حالت های تساوی دو زاویه، تناسب سه ضلع، حالت تساوی یک زاویه و تناسب اضلاع آن دو زاویه، از حالت های تشابه دو مثلث می باشد.
حالت تساوی دو زاویه از پرکاربردترین حالت های تشابه دو مثلث می باشد.





