در این فیلم آموزشی، می خواهیم معادلات درجه سه، چهار و … را با تبدیل آن ها به معادله درجه دوم حل نمائیم.
حل معادلات درجه سه، چهار و بالاتر
در این قسمت با مثال به حل معادلات درجه 3، 4 و بالاتر که به درجه دوم تبدیل می شوند، خواهیم پرداخت.
مثال) معادله زیر را حل نمائید؟
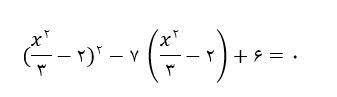
در این مثال تغییر متغیر خواهیم داد. بنابراین معادله درجه چهار بالا به صورت زیر خواهد شد.
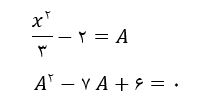
در معادله درجه دوم بالا چون جمع ضرایب صفر است، بنابراین A برابر با شش یا یک خواهد شد.
اگر A=6 باشد، یعنی
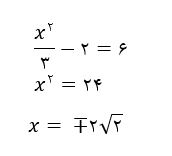
اگر A=1 باشد، یعنی
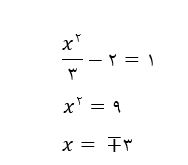
بنابراین معادله مذکور چهار ریشه متمایز دارد.
یکی از روش ها برای حل معادلات درجه سه، چهار و بالاتر تبدیل آن ها به معادله درجه دوم است.
نمونه تست حل معادلات درجه سه، چهار و بالاتر
در این قسمت برای فهم بهتر موضوع حل معادلات درجه سه، چهار و بالاتر به حل تست می پردازیم.
تست) تعداد ریشه های متمایز معادله 2=(x2-2x)-(x2-2x) کدام است؟
- 1
- 2
- 3
- 4
گزینه 3 پاسخ صحیح می باشد.
x2-2x=A را در نظر می گیریم و جایگزین می نمائیم.
A2-A-2=0
اگر در معادله درجه دوم a+c=b باشد، آن گاه یکی از ریشه ها، 1- و ریشه دیگر c/a می باشد. لذا ریشه های این معادله به صورت زیر خواهد بود
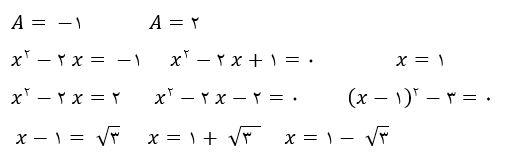
بنابراین معادله دارای سه ریشه متمایز است و گزینه سه صحیح می باشد.
به منظور آشنایی با نمونه تست های بیشتر در مورد موضوع حل معادلات درجه سه، چهار و بالاتر ویدئو آموزشی را مشاهده کنید.
سوالات متداول
یکی از روش ها برای حل این دسته از معادلات، استفاده از معادلات درجه دوم می باشد. در حقیقت می توان با روش هایی مانند تغییر متغیر معادلات مذکور را به معادله درجه دوم تبدیل نمود و سپس آن ها را حل کرد.
اگر در معادله درجه دوم جمع ضرایب صفر شود، یکی از ریشه ها یک و دیگری c/a خواهد بود.





