در این فیلم آموزشی به موضوع محاسبه فاصله نقطه از خط و نمونه تست های آن می پردازیم.
فاصله نقطه از خط چیست؟
منظور از محاسبه فاصله نقطه از خط این است که فاصله عمودی که از نقطه مذکور به خط وارد می شود، چقدر است. فاصله دو خط از یکدیگر، تنها برای خطوط موازی معنی دار می باشد.
فاصله نقطه از خط: فاصله نقطه A به مختصات A(x1, y1) از خط ax+by+c=0 به صورت زیر به دست می آید.
بدین منظور باید، طول عمودی که از نقطه مذکور به خط مورد نظر وارد می شود را محاسبه کنیم.

مثال) فاصله نقطه A(-1,5) از خط 3x-4y-1=0 چقدر است؟
این فاصله از طریق رابطه زیر به دست می آید.
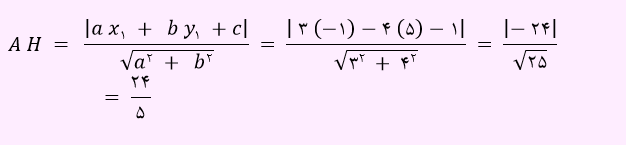
برای فاصله نقطه از خط، باید فاصله عمودی که از نقطه مذکور به خط وارد می شود را محاسبه کنیم.
نمونه تست فاصله نقطه از خط
در این بخش به حل نمونه تست در مورد موضوع فاصله نقطه از خط می پردازیم.
تست 1) خط 5x+12y=1 بر دایره ای به مرکز O ( -1 , 1) مماس است. شعاع این دایره کدام است؟
- 12/13
- 6/13
- 36/169
- 144/169
گزینه 2 پاسخ صحیح می باشد.
شعاع دایره برابر است با طول عمودی که از مرکز دایره به خط 5x+12y-1=0 وارد می شود. بنابراین شعاع دایره به صورت زیر محاسبه خواهد شد.
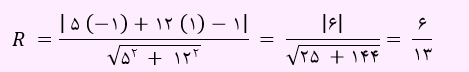
لذا گزینه 2 درست است.
به نمونه تست دوم توجه کنید:
تست 2) یکی از اضلاع مربعی بر خط y=3x-1 واقع است. اگر A(2,-1) یکی از رئوس این مربع باشد، مساحت این مربع چقدر است؟
- 2/4
- 2/6
- 3
- 3/6
گزینه 4 پاسخ صحیح می باشد.
چون مختصات نقطه A(2,-1) ، در خط صدق نمی کند، بنابراین این نقطه روی خط مذکور واقع نمی باشد. در واقع نقطه روی خط مقابل به خط بیان شده، قرار دارد. با به دست آوردن فاصله این نقطه از خط، اندازه ضلع مربع به دست می آید. سپس با توجه به اندازه ضلع مربع، می توان مساحت را به دست آورد. معادله خط به صورت 3x-y-1=0 می باشد.
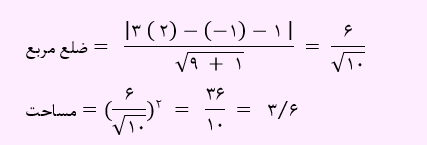
مساحت مربع برابر با 3/6 شد. بنابراین گزینه 4 پاسخ صحیح می باشد.
به منظور یادگیری بیشتر موضوع محاسبه فاصله نقطه از خط و نمونه سوالات تستی آن می توانید ویدئو آموزشی را مشاهده کنید.
سوالات متداول
منظور از فاصله نقطه از خط، فاصله عمودی است که از نقطه به خط وارد می شود.
فرض کنید نقطه A به مختصات A ( x1,y1) و خط مذکور به صورت a x + b y + c = 0 باشد. برای محاسبه فاصله نقطه از خط مذکور، باید حاصل معادله خط به ازای نقطه را بر جذر مجموع توان دوم a و b به دست آوریم.





