در این فیلم آموزشی به حل تست هایی در مورد موضوع زیرمجموعه و شمارش زیر مجموعه ها خواهیم پرداخت.
نمونه تست مجموعه ها و زیر مجموعه ها
به نمونه تست اول در مورد موضوع زیر مجموعه توجه فرمایید:
تست اول) مجموعه {a,b ,{a},{b},{a,b},{b,a}}، چند زیر مجموعه غیر تهی دارد؟
الف) 31
ب) 32
ج) 64
د) 63
گزینه الف پاسخ صحیح می باشد.
عضو {b,a} در مجموعه تکراری است، بنابراین حذف خواهد شد. لذا مجموعه مورد نظر دارای 5 عضو می باشد. پس مجموعه مورد نظر دارای 31=1-25، 31 زیر مجموعه غیر تهی خواهد بود.
به نمونه تست دوم دقت کنید:
تست دوم) مجموعه { x ϵ P|x<15} چند زیر مجموعه حداقل دو عضوی دارد؟ (P مجموعه اعداد اول است)
الف) 26
ب) 27
ج) 57
د) 58
گزینه ج پاسخ صحیح می باشد.
اعضای مجموعه مورد نظر به صورت {2,3,5,7,11,13} می باشد که 6 عضو است.
تعداد زیر مجموعه حداقل دو عضوی به صورت زیر به دست خواهد آمد:
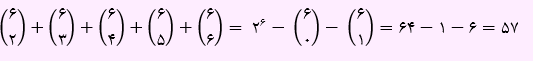
تست بعدی در مورد موضوع تعداد زیر مجموعه می باشد:
تست سوم) مجموعه {a,b ,{a},{b}} دارای چند زیر مجموعه شامل عضو a است؟
الف) 4
ب) 8
ج) 10
د) 12
گزینه ب پاسخ صحیح می باشد.
وقتی که a داخل زیر مجموعه است، a را کنار می گذاریم و با بقیه اعضا زیر مجموعه می نویسیم. پس تعداد زیر مجموعه شامل عضو a برابر با 8=23 خواهد بود.
به نمونه تست چهارم و پنج توجه فرمایید:
تست چهارم) تعداد زیر مجموعه های یک مجموعه 5n+1 عضوی برابر 82n-3 است. این مجموعه چند زیر مجموعه 2 عضوی دارد؟
الف) 45
ب) 36
ج) 210
د) 28
گزینه الف پاسخ صحیح می باشد.
تعداد زیر مجموعه های یک مجموعه 5n+1 عضوی برابر با 25n+1 است. بنابراین رابطه زیر را داریم:
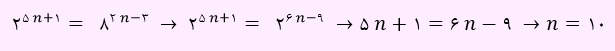
لذا مقدار n برابر با 10 به دست آمد.
تعداد زیر مجموعه 2 عضوی این مجموعه برابر است با:
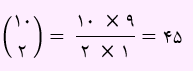
تست پنجم) اگر دو عضو متمایز به مجموعه n عضوی A اضافه کنیم، به تعداد زیر مجموعه های آن 96 زیر مجموعه افزوده می شود. n کدام است؟
الف) 5
ب) 6
ج) 7
د) 4
گزینه الف پاسخ صحیح می باشد.
اگر تعداد اعضا برابر با n باشد، تعداد زیر مجموعه ها مساوی با 2n خواهد شد. اگر تعداد اعضا n+2 شود، تعداد زیر مجموعه ها برابر با 2n+2 خواهد شد. لذا رابطه زیر را داریم:
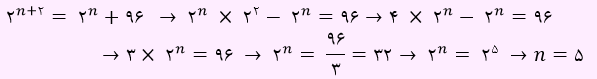
بنابراین مقدار n برابر با 5 می باشد.
به منظور مشاهده نمونه تست های بیشتر در موضوع مجموعه ها و زیر مجموعه ها به ویدئو آموزشی مراجعه کنید.
سوالات متداول
خیر. ترتیب اعضا در مجموعه مهم نمی باشد و اعضای تکراری نیز از مجموعه حذف خواهند شد.
فرض کنید A و B دو مجموعه باشند، اگر حداقل یک عضو از مجموعه A در مجموعه B وجود نداشته باشد، می گوییم A زیر مجموعه B نیست و به صورت زیر بیان می شود:
A ⊈B ⇔ ∃ x ϵ A ⇒x ∉B





