در این فیلم آموزشی با موضوع برآورد بازه ای یا بازه اطمینان و برآورده بازه ای میانگین جامعه آشنا خواهید شد.
برآورد بازه ای یا بازه اطمینان چیست؟
برآورد بازه ای یا بازه اطمینان پارامتر جامعه: بازه ای عددی است برای پارامتر جامعه به همراه یک درصد اطمینان که به ضریب اطمینان معروف است.
برآورد بازه ای برای میانگین جامعه با اطمینان بیش از 95 درصد: اگر نمونه ای تصادفی به اندازه n با میانگین x ̅ وانحراف معیار جامعه σ در اختیار داشته باشیم. بازه ی برآورد برای میانگین جامعه μ با اطمینان بیش از 95 درصد عبارت است از:
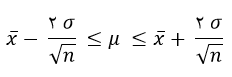
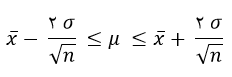
مثال: برای مشاهدات0، 1، 2 و 5 با انحراف معیار 1⁄6داریم:
در این مثال میانگین( x ̅) با 8/4 یعنی 2 برابر می باشد. بنابراین داریم:


به بازه ای عددی برای پارامتر جامعه به همراه یک درصد اطمینان، برآورد بازه ای گفته می شود.
نمونه تست برآورد بازه ای
به نمونه تست زیر توجه کنید:
تست اول) در جامعه ای با انحراف معیار 2⁄5 نمونه ای 100 تایی داریم. اگر میانگین نمونه 10 باشد، برآورد بازه ای میانگین جامعه با اطمینان بیش از 95 درصد کدام است؟
1- (10.5 ,9.5)
2- (10.1 ,9.9)
3- (10.25 ,9.75)
4- (10.05 ,9.95)
گزینه 1 پاسخ صحیح می باشد.
با توجه به صورت سوال داریم:
σ= 2⁄5, n=100, x ̅=10
با توجه به فرمول بازه برآورد داریم:
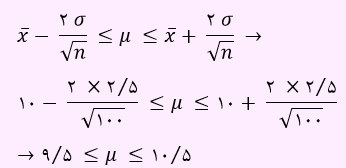
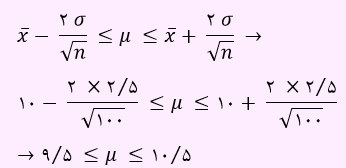
به منظور فهم بهتر موضوع به تست زیر توجه فرمایید:
بنابراین برآورد بازه ای میانگین جامعه با اطمینان بیش از 95 درصد برابر با (10.5 ,9.5) می باشد.
تست دوم) از جامعه ای با واریانس 4⁄41 نمونه {0, 0, 1, 1, 1, 1, 2, 3, 4} انتخاب شده است. برآورد بازه ای میانگین جامعه با اطمینان 95 درصد در کدام بازه قرار دارد؟
1- (2.84 ,0.04)
2- (4.72 ,1.78)
3- (3.7 ,2.3)
4- (4.7 ,3.3)
گزینه 1 پاسخ صحیح می باشد.
با توجه به اینکه واریانس برابر با 4.41 است. برای محاسبه انحراف معیار داریم:
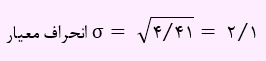
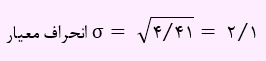
میانگین برابر است با :
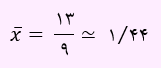
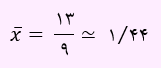
بنابراین برای برآورد بازه ای میانگین جامعه داریم:
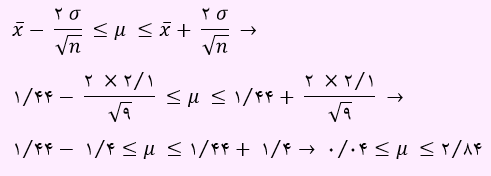
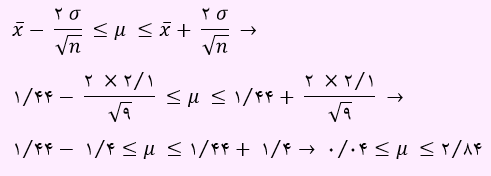
برای آشنایی بیشتر با موضوع برآورد بازه ای یا بازه اطمینان و برآورده بازه ای میانگین جامعه می توانید ویدئو آموزشی را مشاهده کنید.
سوالات متداول
برآورد بازه ای یا بازه اطمینان پارامتر جامعه، به بازه ای عددی برای پارامتر جامعه به همراه یک درصد اطمینان که به ضریب اطمینان معروف می باشد، گفته خواهد شد.




