در این فیلم آموزشی مفاهیم حد تابع، حد چپ، حد راست و نکات آن توضیح داده شده است.
حد تابع چیست؟
در ابتدا به تعریف حد خواهیم پرداخت:
تعریف حد یک تابع: فرض کنیم تابع f در همسایگی X0 به جز احتمالا خود X0 تعریف شده باشد. می گوییم حد تابع f در X به X0 نزدیک می شود برابر عدد حقیقی l است، هر گاه تابع f را به هر اندازه بخواهیم به l نزدیک کنیم به شرط آنکه x از هر دو طرف به قدر کافی به x0 نزدیک شود و می نویسیم: lim f(x)=l x→x0. مقدار l را حد تابع f در x0 می نامیم.
حد یکطرفه
در این بخش، مفهوم حد یکطرفه را توضیح می دهیم.
حد چپ: وقتی x عضو دامنه تعریف f باشد و x با مقادیر کمتر از a به a نزدیک شود به طوری که مقادیر تابع f به l نزدیک شوند، می گوئیم lim f(x)=l x→a– 1. در واقع حد چپ تابع در a برابر l است، هر گاه بتوانیم f را به l نزدیک کنیم، هر گاه x با مقادیر کمتر از a به a نزدیک شود. به همین ترتیب حد راست f در a تعریف می شود.
نکته مهم: اگر f در همسایگی a تعریف شده باشد، f در a دارای حد l است، هر گاه حد چپ و راست f در حالتی که x→a موجود و با هم برابر باشند و مقدار آن ها l باشد. به عبارتی:
به طور مثال y=√x در x=0، حد ندارد. زیرا از سمت چپ x ، نمی تواند به صفر نزدیک شود. y=[x] در x=0 حد ندارد.
تابع y=(x-2)[2x] در x=2 دارای حد است. زیرا:
اولا: f در همسایگی x0=2 تعریف شده است.
ثانیا:
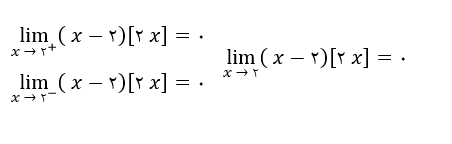
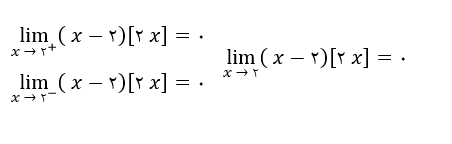
تست: اگر تابع f(x) که در زیر آورده شده است، در x=2 دارای حد باشد، مقدار a کدام است؟
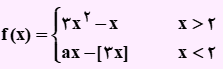
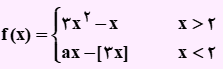
- 2/5
- 10
- 5
- 7/5
گزینه 4 پاسخ صحیح می باشد.
اگر تابع در این نقطه دارای حد باشد، باید حد چپ و راست تابع را در این نقطه به دست آوریم و با یکدیگر برابر قرار دهیم:


به منظور مشاهده نمونه تست های بیشتر در مورد موضوع حد تابع، حد راست و چپ به ویدئو آموزشی مراجعه کنید.
سوالات متداول
اگر یکی از دو شرط زیر برقرار نباشد، تابع در نقطه مذکور حد ندارد.
- باید بتواند از هر دو طرف به عدد نزدیک شود
- عددی که به آن نزدیک می شود، عددی واحد شود.
فرض کنیم تابع f در همسایگی x0 به جز احتمالا خود x0 تعریف شده باشد. می گوییم حد تابع f در x بهx0 نزدیک می شود برابر عدد حقیقی l است، هر گاه تابع f را به هر اندازه بخواهیم به l نزدیک کنیم به شرط آنکه x از هر دو طرف به قدر کافی به x0 نزدیک شود.
وقتی x عضو دامنه تعریف f باشد و x با مقادیر بیشتر از a به a نزدیک شود به طوری که مقادیر تابع f به l نزدیک شوند، می گوئیم lim f(x)=l x→a+ 1. در واقع حد راست تابع در a برابر l است، هر گاه بتوانیم f را به l نزدیک کنیم، هر گاه x با مقادیر بیشتر از a به a نزدیک شود.




