در این فیلم آموزشی به موضوع علامت نسبت های مثلثاتی در نواحی چهارگانه و رابطه شیب خط و تانژانت پرداخته شده است.
علامت نسبت های مثلثاتی در نواحی چهارگانه
علامت نسبت های مثلثاتی در نواحی چهارگانه در جدول زیر نشان داده شده است.


در ناحیه اول، تمام نسبت های مثلثاتی مثبت هستند. از تقسیم علامتهای سینوس و کسینوس بر یکدیگر علامت دو نسبت مثلثاتی تانژانت و کتانژانت به دست خواهد آمد.
دو نسبت مثلثاتی تانژانت و کتانژانت معکوس یکدیگر هستند ولی علامت آن ها در نواحی مختلف دایره مثلثاتی با یکدیگر یکسان می باشد.
در ناحیه دوم، تنها سینوس مثبت می باشد و در ربع چهارم مثلثاتی تنها نسبت کسینوس مثبت است. در ناحیه سوم، هر دو نسبت سینوس و کسینوس منفی هستند، لذا علامت تانژانت و کتانژانت که از تقسیم علامت دو نسبت سینوس و کسینوس به دست می آید، مثبت خواهد شد.
مثال) در هر یک از موارد زیر تعیین کنید θ در کدام ناحیه یا نواحی مثلثاتی قرار دارد؟
الف) sinθ.cosθ<0
با توجه به اینکه حاصل ضرب سینوس در کسینوس منفی است، نیاز است این دو نسبت هم علامت نباشند. در نواحی دوم و چهارم سینوس و کسینوس هم علامت نیستند. بنابراین زاویه مذکور در ربع دوم یا ربع چهارم قرار دارد.
ب) sinθ.tanθ>0
ابتدا نسبت مثلثاتی تانژانت را به صورت حاصل تقسیم سینوس بر کسینوس می نویسیم:


در ربع اول و چهارم مقدار کسینوس مثبت می باشد. لذا زاویه مورد نظر در ربع اول یا ربع چهارم قرار خواهد داشت.
تمام نسبت های مثلثاتی یک زاویه در ربع اول مثبت می باشد.
نمونه تست علامت نسبت های مثلثاتی
به نمونه تست زیر دقت کنید:
تست اول) اگر cosθ=2m-1/4 و θ بین 60º- و 60º حدود m کدام است؟
1- [3/2,5/2]
2- [0,3/2]
3- [1/2,2-]
4- [1/2,5/2-]
گزینه 1 پاسخ صحیح می باشد.
با توجه به اینکه زاویه مورد نظر بین 60- و 60 درجه قرار دارد، در ربع اول و چهارم قرار خواهد داشت. بیشترین مقدار کسینوس بین این دو زاویه برابر با 1 و کمترین مقدار آن برابر با 1/2 می باشد. لذا داریم:
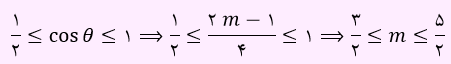
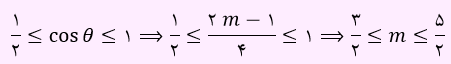
به مثال زیر دقت کنید:
مثال) معادله خطی بنویسید که از نقطه (0,4) بگذرد و با جهت مثبت محور x ها زاویه 30 درجه بسازد؟
با توجه به اینکه معادله خط از نقطه (0,4) می گذرد، عرض از مبدا این خط برابر با 4 است. شیب خط برابر با تانژانت 30 درجه می باشد. پس داریم:
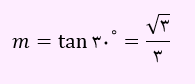
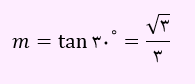
بنابراین معادله خط به صورت زیر می باشد:
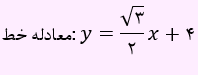
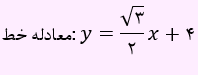
برای آشنایی بیشتر با موضوع علامت نسبت های مثلثاتی در نواحی چهارگانه و نمونه سوالات آن می توانید ویدئو آموزشی را مشاهده کنید.
سوالات متداول
در ربع دوم، علامت تمام نسبت های مثلثاتی شامل کسینوس، تانژانت و کتانژانت منفی می باشد. در این ناحیه تنها علامت نسبت مثلثاتی سینوس مثبت خواهد بود.
شیب هر خط برابر است با تانژانت زاویه ی بین آن خطی که محور افقی را قطع می کند و جهت مثبت محور افقی.
در ربع سوم، دو نسبت مثلثاتی سینوس و کسینوس منفی هستند. بنابراین با توجه به اینکه علامت دو نسبت تانژانت و کتانژانت از تقسیم علامت سینوس و کسینوس به دست می آید، در ربع سوم علامت نسبت های تانژانت و کتانژانت مثبت خواهد بود.




