در این فیلم آموزشی، برای آشنایی بیشتر با مفاهیم حد به حل چند نمونه تست و توضیح قضایای حد خواهیم پرداخت.
قضایای حد
در این قسمت به بررسی قضایای حد می پردازیم.
- حد تابع f(x)=c در هر نقطه دلخواه a برابر مقدار ثابت c است به عبارتی lim f(x)=c x→a
- اگر f(x)=x تابع همانی باشد، آن گاه در هر نقطه دلخواه مانند a ، مقدار limf(x)=a x→a
- هر گاه f و g هر دو در x=a حد داشته باشند، به طوری کهx→a lim f(x)=l1 وlim g(x)=l2 x→a، آن گاه روابط زیر برقرار است:

برای فهم بیشتر قضایای حد به حل یک مثال خواهیم پرداخت.
مثال: اگر دوتابع f(x) و g(x)، به صورت زیر باشند، حد توابع f – 2 ،g و f . g را وقتی x→3 بیابید؟
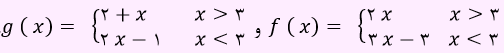
اولا باید بررسی کنیم تابع در نقطه 3 دارای حد باشد. این توابع شرط اول که در طرفین 3 تعریف شده باشند را دارا هستند. حد راست و چپ f در نقطه 3 دارای مقدار یکسان 6 است. حد راست و چپ g در نقطه 3 دارای مقدار برابر 5 هست. لذا هر دو تابع، شرط دوم را نیز دارند. بنابراین هر دو تابع در نقطه 3 دارای حد می باشند.
lim f(x) = 6 x→3
lim g(x)=5 x→3
حال با استفاده از قضایای حد مقدار حد توابع f – 2 ،g و f . g را حساب خواهیم کرد.
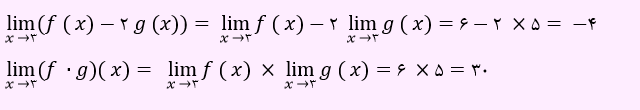
نکته: ممکن است دو تابع دارای حد نباشند، ولی مجموع و ضرب آنها دارای حد باشد.
حد تابع همانی، در هر نقطه دلخواه، برابر با مقدار همان نقطه می باشد.
نمونه تست قضایای حد
در این بخش به حل یک نمونه تست خواهیم پرداخت:
تست: اگر توابع f و g در x=1 دارای حد باشند، به طوری که lim (2f(x)+g(x))=4 x→1 و lim(f(x)-3g(x))=9 x→1، مقدار عبارت زیر کدام است؟
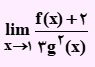
- 1/4
- 3/5
- 5/12
- 2/7
گزینه 3 پاسخ صحیح می باشد.
فرض کنیم lim f(x)=l1 :x→1 lim g(x)=l2 x→1
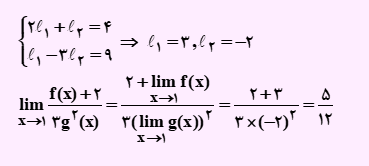
لذا گزینه 3 پاسخ صحیح می باشد.
به منظور آشنایی بیشتر با قضایای حد و نکات آن فیلم آموزشی را مشاهده کنید.
سوالات متداول
اگر تابعی ثابت و مقدارش برابر با c باشد، در آن صورت در هر نقطه دلخواهی مانند a دارای حد بوده و مقدار حد آن مساوی با c خواهد بود. در واقع در تابع ثابت f ( x)=c در هر نقطه دلخواه a مقدار حد برابر مقدار ثابت c می باشد.
مقدار حد تابع همانی در هر نقطه ای برابر با خود نقطه می باشد. در واقع در تابع همانی f ( x)=x، حد در نقطه a برابر با a خواهد بود.
در صورتی که هر دو تابع دارای حد باشند، آن گاه حد مجموع دو تابع برابر با مجموع حدهای دو تابع است.






سلام مورد اول در صورتی درست هست که حد هر یک از توابع f , g در x=a بی نهایت نشود.