در این فیلم آموزشی با موضوع اتحادهای مثلثاتی و تست های آن آشنا خواهید شد.
اتحادهای مثلثاتی زوایای مرکب
اتحادهای مثلثاتی زوایای مرکب: برای سینوس جمع دو زاویه و سینوس تفاضل دو زاویه، رابطه زیر را داریم.
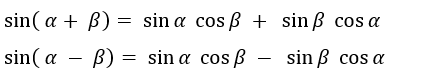
برای کسینوس جمع دو زاویه و تفاضل دو زاویه، رابطه زیر را خواهیم داشت.

به طور مثال برای سینوس جمع دو زاویه 60 و 30 درجه رابطه زیر را خواهیم داشت.
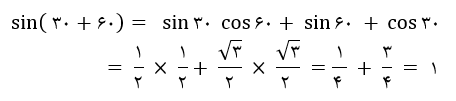
مثال) مقدار هر یک را بیابید؟
sin75°
زاویه 75 درجه را می توان از جمع زوایای 35 و 45 که مقدار نسبت های مثلثاتی آن را می دانیم، به دست آورد. بنابراین مقدار سینوس زاویه 75 درجه را به صورت زیر محاسبه خواهیم کرد.
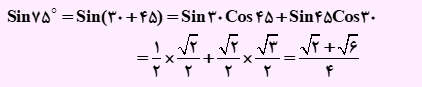
2)cos15°
زاویه 15 درجه را می توان از تفاضل زاویه های 60 و 45 که مقدار نسبت های مثلثاتی آن را می دانیم، به دست آورد. بنابراین مقدار کسینوس زاویه 15 درجه را به صورت زیر محاسبه می کنیم.
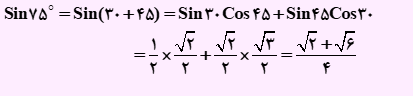
طبق روابط بالا مقدار sin75° و cos15° با یکدیگر برابر شد. علت این موضوع این است که دو زایه 15 و 75 درجه متمم یکدیگر هستند. بنابراین مقدار سینوس یک زاویه با کسینوس دیگری برابر است.
به منظور محاسبه سینوس جمع و تفاضل دو زاویه می توان از اتحادهای مثلثاتی کمک گرفت.
نمونه تست اتحادهای مثلثاتی
در این بخش برای تفهیم بیشتر موضوع نسبت های مثلثاتی زوایای خاص به حل تست می پردازیم.
تست: اگر α و β در نواحی سوم و چهارم باشند به طوری که Cos(π/2+α)=12/13 و Sin(3π/2-β)=-3/5 ، مقدار Cos(α+β) کدام است؟
- 33/65-
- 63/65
- 63/65-
- 5
گزینه 4 پاسخ صحیح می باشد.
با توجه به اتحادهای مثلثاتی داریم:

لذا گزینه 4 پاسخ درست است.
به منظور آشنایی بیشتر با اتحادهای مثلثاتی و نکات آن به ویدئو آموزشی مراجعه کنید.
سوالات متداول
اگر α و β دو زاویه دلخواه باشند، سینوس جمع این دو زاویه با یکدیگر، فرمول زیر را خواهد داشت.
sin(α+β)=sinα cosβ+sinβ cosα
اگر α و β دو زاویه دلخواه باشند، کسینوس تفاضل این دو زاویه با یکدیگر، فرمول زیر را داراست.
cos(α-β)=cosα cosβ+sinα sinβ





