در این فیلم آموزشی با موضوع اجتماع، اشتراک، تفاضل مجموعه ها و برابری مجموعه ها آشنا خواهید شد.
برابری مجموعه ها
دو مجموعه مساوی : دو مجموعه A و B را مساوی گوییم هرگاه هر عضوی از A در B و هر عضوی از B در A موجود باشد. به عبارتی A ⊆B و B ⊆A باشد:
A=B ⟺(A ⊆B ∧ B⊆A)
تست اول) کدام یک از مجموعه های زیر با بقیه متفاوت است؟
الف) { x∈Z│x2≤1}
ب) { x∈Z│x2 ≤x}
ج) { x∈Z│x3-x=0}
د) { x∈Z│|x|<2}
گزینه ب پاسخ صحیح می باشد.
اعضای مجموعه گزینه الف برابر با {1, 0, 1-} می باشد. اعضای مجموعه گزینه ب به شکل {0,1} است. اعضای مجموعه گزینه ج مساوی با {1, 0, 1-} خواهد بود و اعضای مجموعه گزینه د نیز برابر با {1, 0, 1-} می باشد. بنابراین تنها، اعضای مجموعه گزینه ب با بقیه متفاوت است.
به نمونه تست دوم دقت کنید:
تست دوم) اگر دو مجموعه A={{2,z},{0,z,t}} و B={{1,x},{1,x,y}} برابر باشند، حاصل x + y + z +1 کدام است؟
الف) 5
ب) 2
ج) 3
د) 4
گزینه الف پاسخ صحیح می باشد.
باید اعضای دو عضوی و سه عضوی دو مجموعه را با یکدیگر مساوی قرار دهیم، یعنی داریم:
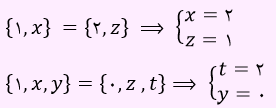
بنابراین حاصل x + y + z +1 برابر با 5 به دست آمد.
به نمونه تست سوم دقت نمایید:
تست سوم) کدام یک از مجموعه های زیر برابر تهی است؟
الف) { x ∈Q | x2+ √(3 x)-6=0}
ب) { x ∈P|3 x+1 ∈P}
ج) {x ∈N| x2-4 x=0}
د) {x ∈Z|2 x=6,x3-9x=0}
گزینه الف پاسخ صحیح می باشد.
گزینه ب دارای عضو {2} می باشد. گزینه ج دارای تک عضو {4} است. گزینه ج نیز دارای یک عضو {3} می باشد. تنها گزینه ای که برابر تهی است، گزینه الف خواهد بود.
دو مجموعه مساوی مجموعه هایی هستند که هر یک زیر مجموعه دیگری باشد.
اجتماع، اشتراک و تفاضل مجموعه ها
در این بخش به اجتماع، اشتراک و تفاضل مجموعه ها می پردازیم.
اجتماع دو مجموعه: اعضایی که حداقل به یکی از دو مجموعه A یا B تعلق دارند. در واقع رابطه زیر را داریم:
A ∪B={x|x ∈A ∨x ∈B}
اشتراک دو مجموعه: اعضایی که به هر دو مجموعه A و B تعلق دارند.
A ∩B={x|x ∈A ∧x ∈B}
تعمیم تعاریف اجتماع و اشتراک به صورت زیر می باشد:
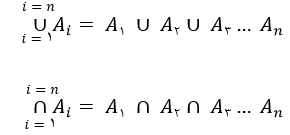
تفاضل دو مجموعه: اعضایی که به مجموعه A تعلق دارند ولی در B نیستند.
A-B={ x|x ∈A ∧x ∉B}
تست) اگر A={x,y,{x,y,z}}، B={x,y,z,{x,y}} و C={x,y,z} کدام رابطه درست است؟
الف) A – B = {C}
ب) B – C = {x,y}
ج) ∅=B – C
د) A – B = C
گزینه الف پاسخ صحیح می باشد.
اگر اعضای مجموعه B را از A کم کنیم، برابر با {C} یعنی {{x,y,z}} خواهد شد.
به منظور یادگیری بیشتر موضوع اجتماع، اشتراک و تفاضل مجموعه ها ویدئو آموزشی را مشاهده کنید.
سوالات متداول
فرض کنید A و B دو مجموعه دلخواه باشند، دو مجموعه A و B مساوی هستند هرگاه هر عضوی از A در B و هر عضوی از B در A وجود داشته باشد. به عبارتی A ⊆B و B ⊆A باشد. برای شرط تساوی دو مجموعه رابطه زیر را داریم:
A=B ⟺(A ⊆B ∧B⊆A)
فرض کنید A و B دو مجموعه دلخواه باشند، اجتماع دو مجموعه برابر است با اعضایی که حداقل به یکی از دو مجموعه A یا B تعلق دارند. رابطه اجتماع به شکل زیر می باشد:
A ∪B={x|x ∈A ∨x ∈B}
فرض کنید A و B دو مجموعه دلخواه باشند، اشتراک دو مجموعه A و B برابر است با اعضایی که به هر دو مجموعه A و B تعلق دارند. در واقع داریم:
A ∩B={x|x ∈A ∧x ∈B}





