در این فیلم آموزشی با موضوع اعمال روی توابع شامل جمع، تفریق، ضرب و تقسیم دو تابع آشنا خواهید شد.
اعمال جبری روی توابع
دو تابع را در صورتی می توان با یکدیگر جمع، تفریق، ضرب و تقسیم نمود که بین دامنه آن ها اشتراک وجود داشته باشد. اگر بین دامنه دو تابع هیچ اشتراکی وجود نداشته باشد، نمی توان بین آن ها هیچ کدام از اعمال را انجام داد.
اگر f و g به ترتیب دو تابع با دامنه های Df و Dg باشند. در این صورت جمع، تفرق، ضرب و تقسیم آن ها را به صورت زیر تعریف می کنیم:

اعمال جبری روی دو تابع در صورتی قابل انجام است که بین دامنه آن ها اشتراک وجود داشته باشد.
نمونه تست اعمال جبری روی توابع
به نمونه تست زیر توجه کنید:
تست) اگر f = { (1,2) , (2, 0), (3, -1)} و g = { (0,3) , (-1, 2), (5, 5)} مجموع اعضای برد تابع 2f+g-1 کدام است؟
- 1-
- 2-
- صفر
- 3-
گزینه 4 پاسخ صحیح می باشد.
تابع 2f یعنی با حفظ دامنه، برد تابع f را در 2 ضرب کنیم. پس تابع 2f به صورت زیر خواهد بود.
2f={(1,4), (2,0), (3,-2)}
برای به دست آوردن تابع g-1 نیز باید جای مولفه های تابع g را تعویض نمود.
g-1={(3,0)(2,-1),(5,5)}
حال باید دو تابع بالا را با یکدیگر جمع کنیم. برای این امر، ابتدا باید بین دامنه های آن اشتراک گرفت و سپس برد دامنه های مشترک را با یکدیگر جمع نمود.
2f+g-1={(3,-2),(2,-1)}
بنابراین مجموع اعضای برد برابر با (1-) + (2-) یعنی 3- خواهد شد.
به نمونه تست دوم توجه کنید:
تست) اگر f(x)=√x و g(x) = { (-1,0) , (-4, 2), (9, 0), (16,1)}. تابع f/g کدام است؟
- {(16,4)}
- {(16,1), (9,0)}
- {(16,16)}
- {(9,9), (16,16)}
گزینه 1 پاسخ صحیح می باشد.
ابتدا باید بین دامنه این دو تابع اشتراک گرفته شود.
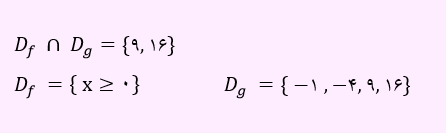
حال تابع f/g را به صورت زیر به دست خواهیم آورد.
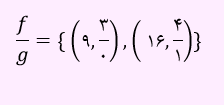
زوج مرتب (9,3/0) بی معناست. بنابراین تابع f/g به صورت زیر می باشد.
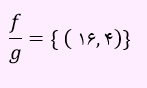
برای آموزش روش محاسبه جمع، تفریق، ضرب و تقسیم دو تابع ویدئو آموزشی این جلسه را مشاهده نمایید.
سوالات متداول
اولین شرط برای اینکه دو تابع را بتوان با یکدیگر جمع نمود، این است که دامنه دو تابع اشتراک داشته باشند.
برای اینکه دو تابع را بتوان تقسیم نمود، اولا باید بین دامنه آن ها اشتراک وجود داشته باشد، ثانیا مخرج مخالف صفر باشد.
دامنه حاصل ضرب دو تابع مساوی با اشتراک دامنه دو تابع می باشد. در واقع در صورتی می توان دو تابع را در یکدیگر ضرب نمود که بین دامنه آن ها اشتراک وجود داشته باشد.





