در این فیلم آموزشی به موضوع برآورد بازه ای نسبت با اطمینان 95 درصد و نکات آن پرداخته شده است.
برآورد بازه ای نسبت با اطمینان 95 درصد
تست اول) با انتخاب یک نمونه 400 عضوی از دانش آموزان یک مدرسه دولتی تعداد 40 تای آن ها قصد ترک تحصل دارند. بازه اطمینان نسبت واقعی دانش آموزانی که قصد ترک تحصیل دارند با اطمینان 95 درصد در این مدرسه کدام است؟
1- 13 – 7
2- 14 – 8
3- 12 – 6
4- 15 – 9
گزینه 1 پاسخ صحیح می باشد.
در این تست n برابر با 400 و m مساوی با 40 است. بنابراین داریم:
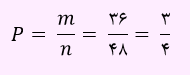
برای بازه اطمینان داریم:
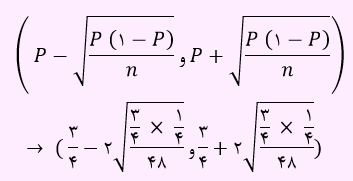
به بازه ای عددی برای پارامتر جامعه به همراه یک درصد اطمینان، برآورد بازه ای گفته می شود.
نمونه تست برآورد بازه ای
به نمونه تست زیر توجه کنید:
تست اول) با انتخاب یک نمونه 400 عضوی از دانش آموزان یک مدرسه دولتی تعداد 40 تای آن ها قصد ترک تحصل دارند. بازه اطمینان نسبت واقعی دانش آموزانی که قصد ترک تحصیل دارند با اطمینان 95 درصد در این مدرسه کدام است؟
1- 13 – 7
2- 14 – 8
3- 12 – 6
4- 15 – 9
گزینه 1 پاسخ صحیح می باشد.
در این تست n برابر با 400 و m مساوی با 40 است. بنابراین داریم:
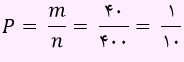
برای بازه اطمینان داریم:
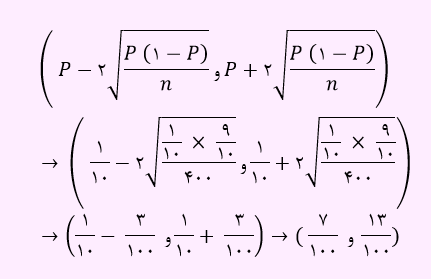
لذا بازه اطمینان نسبت واقعی دانش آموزانی که قصد ترک تحصیل دارند با اطمینان 95 درصد در این مدرسه برابر با 13 – 7 خواهد بود.
به منظور فهم بهتر موضوع به تست زیر توجه فرمایید:
تست دوم) در یک آزمایش تصادفی برای تشخیص نسبت افراد سیگاری به کل افراد، تعداد نمونه های آزمایشی را 100 برابر می کنیم. بازه اطمینان 95 درصد چند برابر می شود؟
1- 0.1
2- 10
3- 10√
4- 3
گزینه 1 پاسخ صحیح می باشد.
با توجه به اینکه اگر تعداد نمونه ها k برابر شود، طول بازه اطمینان یک تقسیم بر 10√ برابر می شود، بازه اطمینان یک تقسیم بر 100√ یعنی 0⁄1 برابر خواهد شد.
برای فهم بیشتر موضوع برآورد بازه ای نسبت با اطمینان 95 درصد می توانید ویدئو آموزشی را مشاهده کنید.
سوالات متداول
در برآورد بازه ای نسبت با اطمینان 95 درصد، اندازه بازه وابسته به اندازه نمونه می باشد و به اندازه جامعه ربطی ندارد.
به منظور افزایش بازه اطمینان به بالای 95 درصد کافیست در بازه، ضریب 2 را بزرگ تر قرار دهیم.





