در این فیلم آموزشی در مورد تابع وارون، به دست آوردن ضابطه تابع وارون یک تابع خطی غیر ثابت توضیح داده شده است.
تابع وارون چه تابعی است؟
وارون تابع: با جا به جا کردن مولفه های زوج مرتب (a, b) می توان زوج مرتب (b, a) را به دست آورد. اگر برای همه زوج مرتب های یک تابع مانند f این کار را انجام دهیم تابع f -1 به دست می آید. به تابع f-1، تابع وارون گفته می شود.
نکته: اگر تابع f یک به یک باشد، آن گاه تابع f وارون پذیر است و بالعکس.
مثال: وارون تابع f = {(1,2) , (3, -5), (0, 0)} را به دست آورید؟
چون تابع یک به یک است، بنابراین وارون دارد. برای به دست آوردن وارون تابع مذکور، باید جای زوج مرتب های آن را تعویض نمود.
f-1={(2,1), (-5,3), (0,0)}
به نمونه تست زیر توجه کنید:
تست) اگر در تابع f={(2, a3+1), (b+5, 3)} داشته باشیم، f=f-1 حاصل ab کدام است؟
- 2-
- 2
- 3-
- 3
گزینه 1 پاسخ صحیح می باشد.
ابتدا وارون تابع را به دست می آوریم.
f-1={(a3+1, 2), (3, b+5)}
f={(2, a3+1), (b+5,3)}
برای اینکه این دو تابع یعنی f و f-1 برابر باشند، باید دامنه آن ها مساوی باشد. لذا a3+1 ، باید برابر با 2 و b+5 مساوی با 3 باشد.
a3+1=1 a3=1 a=1
b+5=3 b=-2
بنابراین حاصل ab برابر با 2- خواهد بود.
نکته: نمودار هر تابع و وارون آن نسبت به نیمساز ناحیه اول و سوم ( خط y = x) قرینه یکدیگر هستند.
تابع وارون تابعی است که با جا به جا کردن تمام زوج مرتب های یک تابع به دست می آید.
به دست آوردن ضابطه تابع وارون یک تابع خطی غیر ثابت
به دست آوردن ضابطه تابع وارون یک تابع خطی غیر ثابت: برای تعیین وارون تابع خطی f ( x) = a x + b ( با شرط a≠0) ابتدا از رابطه y = a x + b، مقدار x را بر حسب y به دست آورده سپس جای x و y را عوض می کنیم.
مثال: وارون تابع خطی زیر را تعیین کنید؟
ابتدا باید x را بر حسب y به دست آوریم. در نهایت جای x و y را عوض نمائیم.
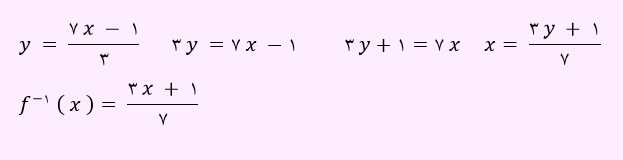
برای یادگیری بیشتر موضوع تابع وارون و به دست آوردن ضابطه تابع وارون ویدئو آموزشی را مشاهده کنید.
سوالات متداول
اگر برای همه زوج مرتب های یک تابع مانند f ، جای مولفه های زوج مرتب آن را تعویض نمود، تابع f-1 به دست می آید. به تابع f-1، تابع وارون گفته خواهد شد. تابع f در صورتی وارون پذیر است که یک به یک باشد.
برای رسم نمودار وارون یک تابع، باید نمودار تابع را نسبت به خط y = x قرینه نمود. زیرا نمودار هر تابع و وارون آن نسبت به خط y =x قرینه هم هستند.
برای به دست آوردن ضابطه تابع وارون یک تابع خطی غیر ثابت مانند f ( x) = a x + b ( با شرط a ≠0) ابتدا، x را بر حسب y به دست می آوریم و در نهایت جای x و y را عوض خواهیم کرد.






عالی خیلی ممنون
سلام
امیدواریم مبحث تابع وارون و محاسبه ضابطه آن را به خوبی فرا گرفته باشید.