تابع پله ای، تابع جزء صحیح چیست؟

در این فیلم آموزشی با توابع پله ای، جزء صحیح و دامنه آن ها آشنا خواهید شد.

پخش ویدئو

تابع پله ای و جزء صحیح چیست؟

تابع پله ای: به توابعی مانند تابع زیر که در بازه های مختلف ضابطه آن ها تابعی ثابت است “تابع پله ای” می گویند. معروف ترین تابع پله ای، تابع جز صحیح است.

تابع جز صحیح: ضابطه این تابع به صورت است که به هر عدد صحیح، خود آن عدد صحیح و به هر عدد غیر صحیح، بزرگ ترین عدد صحیح کوچک تر از آن را نسبت می دهد.

تابع جز صحیح: ضابطه این تابع به صورت f(x)=[x] است که به هر عدد صحیح، خود آن عدد صحیح و به هر عدد غیر صحیح، بزرگ ترین عدد صحیح کوچک تر از آن را نسبت می دهد.

مثال: جز صحیح اعداد زیر را بنویسید.

[5]=5

[5/1]=5

[5/95]=5

در این بخش ویژگی های جز صحیح را بررسی خواهیم کرد.

نکته : اگر k∈Z و [x]=k نتیجه می شود k≤x<k+1

نکته: اگر k∈Z در این صورت داریم :

[x±k]=[x]±k

تابع پله ای تابعی است که در بازه های مختلف، ضابطه آن تابعی ثابت می باشد.

نمونه تست توابع پله ای و جزء صحیح

به نمونه تست های زیر توجه کنید:

تست) حاصل عبارت زیر کدام است؟

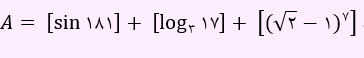
1
2
3
صفر

گزینه 1 پاسخ صحیح می باشد.

sin181 در ربع سوم قرار دارم و در ربع سوم، سینوس منفی است. بنابراین مقدار آن برابر با …/0- است. پس جز صحیح [sin181] مساوی با 1- می باشد. مقدار log 17 در مبنای 3 مساوی با 2 و خرده ای است. بنابراین جز صحیح آن برابر با 2 خواهد بود. مقدار ⁷(1-2√) مساوی صفر و خرده ای است. لذا جز صحیح آن برابر با صفر می شود. بنابراین حاصل عبارت A به صورت زیر خواهد شد.

A=-1+2+0=1

لذا حاصل A برابر با 1 به دست آمد.

به نمونه تست دوم توجه کنید:

تست) مجموعه جواب معادله 15= [x-1]+[x+2[x]] کدام است؟

(3,4]
(4,5]
[15,16]
(16,17]

گزینه 2 پاسخ صحیح می باشد.

چون 1- عدد صحیح است، می تواند از داخل جز صحیح [x-1] بیرون بیاید. همچنین [x]2 نیز عدد صحیح بوده و از داخل [x+2[x]] می تواند بیرون کشیده شود. لذا روابط زیر را خواهیم داشت:

[x-1]+[x+2[x]]=15 [x]-1+[x]+2[x]=15 4[x]=16 [x]=4

بنابراین بازه x به صورت (4,5] می باشد.

برای شناخت بیشتر تابع پله ای، تابع جزصحیح و یافتن دامنه آنها ویدئوی آموزشی این جلسه را مشاهده نمایید.