در این فیلم آموزشی به حل نمونه سوال و تست مبحث اتحادهای مثلثاتی زوایای مرکب می پردازیم.
نمونه تست اتحادهای مثلثاتی زوایای مرکب
در ابتدا با یک نمونه سوال مهم که در تست های کنکور سراسری بسیار تکرار شده است، شروع خواهیم کرد.
سوال) به فرض آنکه tan(α+β)=1/2 و α-β=2Π/3 ، حاصل عبارت زیر چه عددی است؟
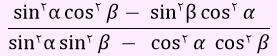
برای صورت و مخرج عبارت داده شده ، اتحاد مزدوج را به صورت زیر می نویسیم.
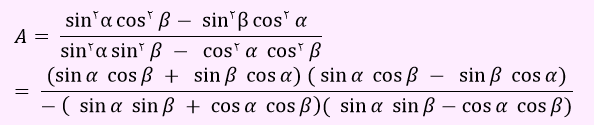
حال در عبارت بالا، sinαcosβ+sinβcosα ، برابر با ، sin(α+β) عبارتsinαcosβ-sinβcosα ، مساوی با ، sin(α+β) ، عبارت sinαsinβ+cosαcosβ برابر با cos(α-β)cos(α+β) و sinαsinβ-cosαcosβ، مساوی با cos(α+β) خواهد بود. بنابراین در عبارت بالا، موارد ذکر شده را جایگزین خواهیم کرد.
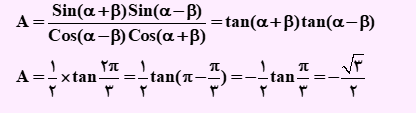
در ادامه به حل یک تست می پردازیم:
تست) مقدار tan40°(tan50°+tan20°) چه عددی است؟
- 1
- cos20°
- 1/2
- tan20°
گزینه 1 پاسخ صحیح می باشد.
برای tanα+tanβ ، فرمول زیر را داریم.
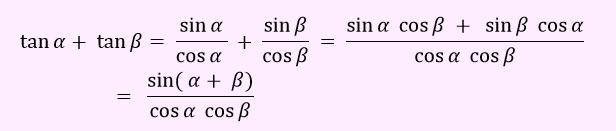
به جای tan50+tan20 ، از رابطه بالا استفاده می کنیم و حاصل را به شکل زیر قرار خواهیم داد.
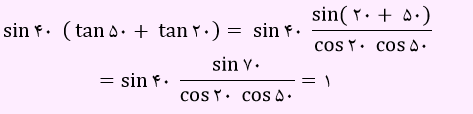
در رابطه بالا، sin70 و cos20 چون متمم یکدیگر هستند، با یکدیگر ساده شدند. sin40 و cos50، نیز متمم یکدیگر هستند، پس با هم ساده خواهند شد.
بنابراین گزینه 1 پاسخ صحیح می باشد.
سینوس و کسینوس دو برابر یک زاویه از جمله اتحادهای مهم مثلثاتی است.
اتحادهای مثلثاتی
در این قسمت به بیان چند نمونه دیگر از اتحادهای مهم مثلثاتی می پردازیم:
چند نمونه از اتحادهای مثلثاتی مهم در زیر عنوان شده است.
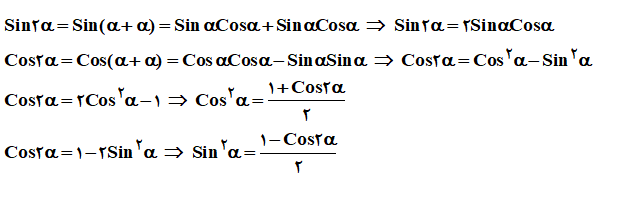
به فرض آنکه x در ناحیه اول باشد و sin(Π/2-x)=1/3 ، حاصل cos(2x+Π/3) چه عددی است؟
با توجه به اتحادهای مثلثاتی بیان شده، حاصل عبارت داده شده به صورت زیر خواهد بود:
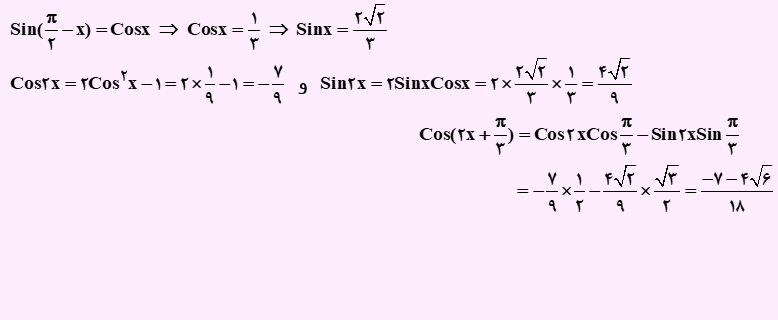
به منظور آشنایی با نمونه تست های بیشتر در مورد موضوع اتحادهای مثلثاتی به ویدئو آموزشی مراجعه کنید.
سوالات متداول
اگر فرض کنیم، α و β دو زاویه باشند. برای محاسبه tanα- tanβ، باید sin( α- β) را بر cosα cosβ تقسیم کنیم.
برای سینوس دو برابر زاویه دلخواهی مانند α، می توان رابطه زیر را نوشت.
sin2 α= 2 sinα cos α





