در این فیلم آموزشی به موضوع جایگشت و نمونه تست های آن پرداخته شده است.
جایگشت چیست؟
جایگشت: به هر حالت قرار گرفتن n شی متمایز در کنار هم یک جایگشت از آن اشیا می گوییم. گاهی اوقات n شی متمایز داریم و قرار است k تای آن ها را در کنار هم قرار دهیم. ( K≤n)
مثال) با حروف کلمه “دانشجو” چند کلمه سه حرفی می توانیم بنویسیم؟
کلمه “دانشجو” دارای شش حرف “د، ا، ن، ش، ج، و” می باشد. بنابراین انتخاب اول دارای 6، انتخاب دوم 5 و انتخاب سوم دارای 4 حالت است. بنابراین تعداد کل حالات برابر با 6×5×4 یعنی 120 خواهد بود.
مثال) با حروف کلمه “درمان” چند کلمه 3 حرفی، 4 حرفی بدون تکرار ارقام، می توانیم بنویسیم؟
کلمه “درمان” دارای پنج حرف “د، ر، م، ا، ن” می باشد. بنابراین تعداد کلمات 3 حرفی برابر با 5×4×3 یعنی 60 بوده و تعداد کلمات 4 حرفی برابر با 5×4×3×2 یعنی 120 خواهد بود.
در این بخش به معرفی چند نماد خواهیم پرداخت.
تعداد جایگشت r شی از بین n شی متمایز به شرطی که ترتیب قرار گرفتن مهم باشد، از رابطه زیر به دست می آید:
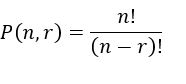
می خواهیم از بین 10 کتاب، 4 کتاب رادر قفسه ای بچینیم. از چه رابطه ای استفاده می کنیم؟
در این مسئله، ترتیب قرار گرفتن مهم است. لذا از رابطه زیر استفاده خواهیم کرد:

به هر حالت قرار گرفتن n شی متمایز در کنار هم یک جایگشت از آن اشیا گفته خواهد شد.
نمونه تست جایگشت
به نمونه تست اول توجه کنید:
تست اول) با حروف کلمه ORGINAL یک کلمه 7 حرفی می نویسم. در چند حالت کلمه OIL دیده می شود؟
1- !5 × !2
2- !5 × !3
3- !5 × !3 × !2
4- !5
گزینه 4 پاسخ صحیح می باشد.
با توجه به صورت سوال سه حرف O، I و L باید به صورت OIL کنار هم باشند. پس این سه حرف را به صورت 1 بسته در نظر می گیریم که با چهار حرف دیگر (R, G, N, A)، حالت جایگشت دارند.
برای آشنایی بیشتر با موضوع جایگشت و نمونه سوالات آن می توانید ویدئو آموزشی را مشاهده کنید.
سوالات متداول
جایگشت به نوعی انتخاب محسوب می شود. به منظور انتخاب k شی از بین n شی از جایگشت استفاده خواهد شد. در واقع به هر حالت قرار گرفتن n شی متمایز در کنار هم یک جایگشت از آن اشیا گفته خواهد شد.
برای محاسبه تعداد جایگشت r شی از بین n شی متمایز به شرطی که ترتیب قرار گرفتن مهم باشد، باید حاصل تقسیم n فاکتوریل را بر فاکتوریل تفاضل r از n محاسبه کنیم.





