در این فیلم آموزشی به موضوع حد توابع مثلثاتی، حل تست در مورد موضوع رفع ابهام خواهیم پرداخت.
حد توابع مثلثاتی
ابتدا این بخش را با حل یک نمونه تست آغاز خواهیم کرد.
تست) اگر عبارت زیر را داشته باشیم، مقدار a – b کدام است؟
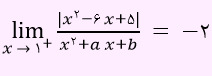
- 1
- 1-
- 7
- 7-
گزینه 4 پاسخ صحیح می باشد.
ابتدا عبارت داخل قدر مطلق را به صورت زیر تجزیه می کنیم.
x2-6x+5=(x-1)(x-5)
با توجه به اینکه x به سمت +1 میل می کند، حاصل (x-1)، مثبت و (x-5) منفی خواهد بود. لذا کل عبارت داخل قدر مطلق منفی می شود. بنابراین عبارت از داخل قدر مطلق با علامت منفی بیرون می آید.
|x2-6x+5|=-(x-1)(x-5)
چون در صورت عبارت (x-1) وجود دارد. حرکت x به سمت +1 ، صورت را صفر خواهد کرد. چون حد دارای مقدار غیر صفر است، مخرج باید به ازای x=1 ، برابر صفر شود. بنابراین رابطه زیر را داریم.
1+a+b=0 b=-a-1
حال به جای b، مقدار بالا را قرار می دهیم و عبارت زیر به دست خواهد آمد.
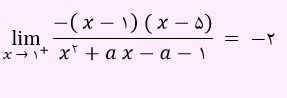
حال مخرج را تجزیه می کنیم.
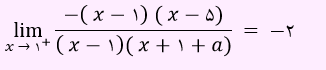
در این صورت در عبارت بالا، می توان عامل ابهام (x-1) را حذف نمود.
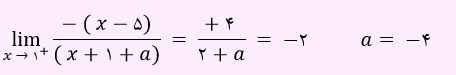
از رابطه بالا a=-4 به دست آمد. بنابراین مقدار b برابر با 3 و حاصل a-b مقدار 7- خواهد شد. بنابراین گزینه 4 پاسخ صحیح می باشد.
در این بخش به موضوع حدود مثلثاتی خواهیم پرداخت.
حدود مثلثاتی دارای روابط زیر خواهد بود.

حد سینوس و کسینوس هر نقطه ای، با مقدار سینوس و کسینوس آن نقطه برابر است.
نمونه تست رفع ابهام حد توابع مثلثاتی
در این بخش موضوع رفع ابهام حدود مثلثاتی را با یک نمونه تست توضیح خواهیم داد.
تست) مقدار عبارت زیر کدام است؟
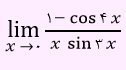
- 8/3
- 4/3
- 1/2
- 2/3
گزینه 1 پاسخ صحیح می باشد.
با توجه به جایگذاری روابط مثلثاتی عبارت به صورت زیر خواهد بود:
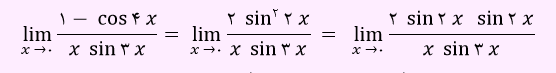
طبق نکاتی که داشتیم، حد sin2x/x برابر با 2 و حد sin2x/sin3x مساوی با 2/3 می باشد. پس عبارت به صورت زیر می باشد.
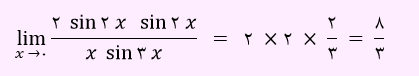
لذا گزینه 1 درست است.
به منظور آشنایی بیشتر با حد توابع مثلثاتی، نمونه تست ها و نکات آن ویدئو آموزشی را مشاهده کنید.
سوالات متداول
مقدار حد تانژانت x تقسیم بر x، زمانی که x به سمت صفر میل کند، برابر با یک خواهد شد.
هنگامی که x به سمت صفر میل می کند، مقدار حد سینوس x تقسیم بر x برابر با یک خواهد بود.





