در این فیلم آموزشی با موضوع دوران در هندسه، ویژگی های دوران و نکات تستی آن آشنا خواهید شد.
دوران در هندسه چیست؟
دوران به مرکز نقطۀ ثابت O و زاویۀ a تبدیلی است که تحت آن تصویر هر نقطه مانند A از صفحه، نقطهای مانند ‘A از همان صفحه است، به طوری که:
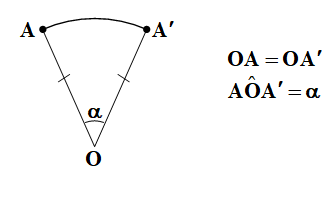
نقطۀ O را مرکز دوران و زاویۀ α را از زاویۀ دوران مینامیم
ویژگی های دوران
ویژگیهای دوران:
1) دوران تبدیلی طولپاست.
2) دوران شیب خط را حفظ میکند، مگر آنکه زاویۀ دوران kΠ باشد.
3) در دوران مرکز دوران، نقطۀ ثابت دوران است.
4) دوران با زاویۀ 2kΠ هر نقطه را بر خودش تصویر میکند.
5) دوران جهت شکل را حفظ میکند.
6) دورانیافتۀ هر خط، خطی است که با خط اول همان زاویۀ دوران را میسازد.
7) هر دو خط موازی دورانیافتۀ یکدیگرند با زاویۀ Π(2k+1) به طوری که مرکز دوران روی خط وسط آن دو خط قرار دارد.

8) هر دو خط متقاطع دورانیافتۀ یکدیگرند به طوری که زاویۀ دوران یکی از زوایای بین دو خط و مرکز دوران روی نیمساز زاویۀ دیگر بین دو خط است.

دوران یک تبدیل طولپا می باشد.
نمونه تست دوران
به نمونه تست زیر دقت کنید:
تست (سرارسی 94)): نقطۀ A و دو دایره در یک صفحه مفروضاند. برای رسم مثلث قائمالزاویه و متساویالساقین به رأس A که دو سر قاعده بر روی هر یک از این دایرهها باشد، کدام تبدیل هندسی به کار میرود؟
1- بازتاب
2- انتقال
3- تجانس
4- دوران
پاسخ : گزینه 4 پاسخ صحیح می باشد.
مطابق شکل مثلث ‘AMM قائمالزاویه و متساویالساقین است. پس دورانیافتۀ نقطۀ M به مرکز A و زاویۀ °90، نقطۀ ‘M است. اگر دایرۀ C را حول نقطۀ A، به اندازه °90 دوران دهیم تا دایرۀ ”C به دست آید، چون تصویر M باید روی این دایره باشد، پس ‘M محل تلاقی دو دایرۀ ‘C و ”C است و به این ترتیب با دوران، موقعیت ‘M به دست میآید و مثلث ‘AMM رسم میشود.

برای مشاهده نمونه تست های بیشتر در مورد موضوع دوران و نکات آن می توانید به ویدئو آموزشی مراجعه کنید.
سوالات متداول
بله، دوران یکی از تبدیل های طولپا می باشد.
دوران شیب خط را حفظ خواهد کرد. مگر اینکه زاویه دوران KΠ باشد.





