در این فیلم آموزشی با رفع ابهام حد و رفع ابهام صورت صفر صفرم آشنا خواهید شد.
رفع ابهام حد و صورت صفر صفرم
اگر حد تابع های f و g در نقطه a برابر صفر باشد و تابع های f و g در اطراف a، تابع ثابت صفر نباشند، آن گاه برای محاسبه lim f(x)/g(x)، x→a در نقطه a باید عامل صفر کننده را از صورت و مخرج پیدا کرده و آن ها را حذف کنیم. به این کار “رفع ابهام صورت صفر صفرم ” می گویند.
مثال: حد تابع زیر را بیابید؟

زمانی که x به سمت 1 میل کند، هم صورت و هم مخرج صفر خواهد شد. بنابراین نیاز است عامل صفر را از صورت و مخرج استخراج کنیم. هنگامی که x به سمت a میل کند، معمولا عامل صفر x – a می باشد. صورت و مخرج را به کمک اتحاد مزدوج و چاق و لاغر به صورت زیر تجزیه خواهیم کرد.

بنابراین مقدار حد تابع برابر با 2/3 شد.
به منظور محاسبه برخی از حدها نیاز است حد چپ و راست مجزا حساب شود.
نمونه تست رفع ابهام حد
به نمونه تست اول توجه کنید:
تست اول) حاصل عبارت زیر کدام است؟
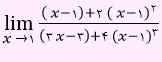
الف) صفر
ب) 1/2
ج) 1/3
د) 1/4
گزینه 3 پاسخ صحیح می باشد.
هنگامی که x به سمت 1 میل کند، هم صورت و هم مخرج صفر خواهند شد. پس نیاز است عامل صفر کننده را حذف کنیم.

حال می توان عامل صفر کننده را از صورت و مخرج حذف نمود.

بنابراین حاصل حد عبارت، برابر با 1/3 به دست آمد.
به نمونه تست دوم دقت نمایید:
تست دوم) حاصل عبارت زیر کدام است؟

الف) 13/12-
ب) 1
ج) 13/14-
د) 7/6-
گزینه 1 پاسخ صحیح می باشد.
وقتی عبارت به سمت 2 میل کند، صورت و مخرج صفر خواهند شد. بنابراین باید عامل ابهام را حذف نمائیم. صورت را به عبارت (x – 2)، تقسیم می کنیم.

حال عامل صفر کننده را از صورت و مخرج حذف می کنیم.

بنابراین مقدار حد برابر با 13/12- شد.
برای فهم بیشتر موضوع به نمونه تست بعدی توجه فرمایید:
تست سوم) حاصل عبارت زیر کدام است؟

الف) 1/108
ب) 1/108-
ج) 1/54
د) 1/54-
گزینه 4 پاسخ صحیح می باشد.
در این حالت، صورت و مخرج برابر صفر می شوند. پس نیاز به رفع ابهام می باشد.

حال عامل صفر کننده را حذف خواهیم کرد.

بنابراین مقدار حد تابع برابر با 1/54- شد.
به منظور مشاهده نمونه تست های بیشتر در مورد موضوع رفع ابهام حد می توانید فیلم آموزشی را مشاهده کنید.
سوالات متداول
به منظور رفع ابهام نیاز است، عامل صفر کننده صورت و مخرج را پیدا کرده و آن را حذف کنیم.
زمانی که صورت و مخرج کسر مساوی صفر شوند و x به سمت a میل کند، معمولا عامل صفر کننده x – a خواهد بود.





