در این فیلم آموزشی به بررسی رفع ابهام در محاسبه حد و ادامه قضایای حد خواهیم پرداخت.
حد توابع رادیکالی و مثلثاتی
در این بخش به چگونگی محاسبه حد عبارت دارای رادیکال و توابع مثلثاتی می پردازیم:
- فرض کنید f در a دارای حد و در همسایگی a نامنفی باشد آن گاه داریم:

مقدار حد و مقدار f باید نا منفی باشند تا رابطه بالا برقرار باشد.
- در رابطه با حد سینوس و کسینوس یک نقطه فرمول زیر برقرار می باشد.

مثال: حاصل عبارت زیر را به دست آورید؟
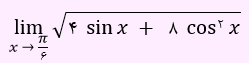
با توجه به قضایای بیان شده داریم:
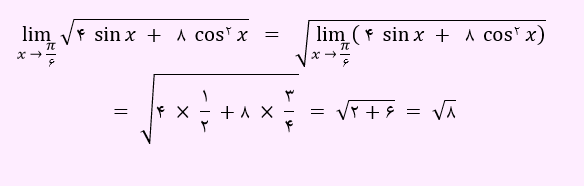
حد سینوس و کسینوس هر نقطه ای، با مقدار سینوس و کسینوس آن نقطه برابر است.
رفع ابهام در محاسبه حد
در این بخش به موضوع رفع ابهام در محاسبه حد می پردازیم.
میخواهیم limf(x)/g(x) x→a را در حالتی پیدا کنیم که lim f(x)=0 x→a و lim g(x)=0 x→a. این حالت را حالت ابهام در محاسبه حد می گوییم و درصدد رفع این ابهام هستیم.
مثال: حد تابع زیر را بیابید.
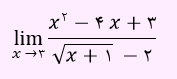
در تابع بالا، وقتی x به سمت 3 میل کند، صورت و مخرج صفر خواهد شد. بنابراین این حالت مبهم هست و باید درصدد رفع آن باشیم. در واقع عامل ابهام را به صورت زیر از صورت و مخرج حذف می کنیم.
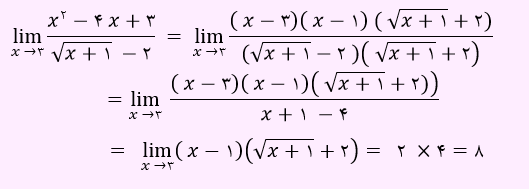
در این بخش به حل یک نمونه تست خواهیم پرداخت:
تست: حاصل عبارت زیر کدام است؟
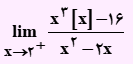
- 24
- 12
- 8
- وجود ندارد
گزینه 2 پاسخ صحیح می باشد.
با توجه به روابط بیان شده داریم:
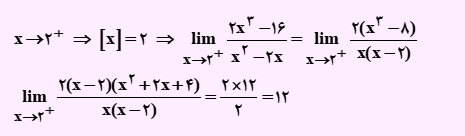
لذا گزینه 2 درست است.
به منظور یادگیری بیشتر موضوع رفع ابهام در محاسبه حد و نکات آن ویدئو آموزشی را مشاهده کنید.
سوالات متداول
اگر در محاسبه حد، x به سمت a حرکت کند و حد به حالت 0/0 برسد، به این حالت مبهم گفته می شود. حالت ابهام قابل رفع می باشد. در این حالت، نیاز است عامل ابهام را از صورت و مخرج حذف کنیم تا ابهام رفع گردد و رفع ابهام منجر به یافتن مقدار حد گردد.
مقدار حد ریشه n ام یک تابع برابر با ریشه n ام حد آن تابع می باشد.
حد سینوس و کسینوس هر نقطه ای با مقدار سینوس و کسینوس آن نقطه برابر است.





