در این فیلم آموزشی به موضوع شرط توازی، شرط عمود بودن دو خط و نکات آن خواهیم پرداخت.
شرط توازی و عمود بودن دو خط
در ابتدا وضعیت دو خط نسبت به یکدیگر را بررسی خواهیم کرد.
شرط موازی بودن دو خط y=mx+n و y=m’x+n’1 آن است که شیب آن ها برابر باشد.
شرط عمود بودن دو خط y=mx+n و y=m’x+n’1 آن است که mm’=-1 باشد.
مثال: اگر دو خط y=3x+5 و y=(m-1)x-7 با هم موازی باشند، m چه مقداری است؟
چون دو خط با یکدیگر موازی هستند، پس باید شیب آن ها با یکدیگر برابر باشد. یعنی داریم:
m-1=3 m=4
بنابراین m باید برابر با 4 باشد.
برای تفهیم بیشتر موضوع به حل مثال دیگری خواهیم پرداخت.
مثال) اگر دو خط y=mx+m+1 و y=x/2+m-2 بر هم عمود باشند، m چه عددی است؟
چون دو خط عمود بر یکدیگر هستند، بنابراین ضرب شیب آن ها باید 1- شود.
m×1/2=-1 m=-2
بنابراین نیاز است m برابر با 2- باشد.
شرط موازی بودن دو خط، این است که شیب دو خط با یکدیگر برابر باشد.
نمونه تست شرط توازی و عمود بودن دو خط
در این بخش به حل نمونه تست در مورد وضعیت دو خط نسبت به یکدیگر خواهیم پرداخت.
تست) مربع ABCD با رئوس A ( 6, 1) و B( 11, 4) را در نظر بگیرید. معادله ضلع AD کدام است؟
- 3x+5y=33
- 3x+5y=23
- 3x-5y=13
- 5x-3y=33
گزینه 1 پاسخ صحیح می باشد.
برای نوشتن معادله خط AD، نیاز به یک نقطه داریم. نقطه A را داریم. علاوه بر نقطه شیب خط AD را نیز نیاز داریم. دو خط AB و AD بر یکدیگر عمود هستند. ابتدا شیب خط AB را به دست می آوریم.
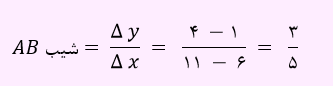
از آنجایی که دو خط AB و AD بر یکدیگر عمود هستند، بنابراین شیب خط AD برابر است با 5/3-. حال می توان معادله ضلع AD را نوشت.

معادله خط از طریق رابطه بالا به دست آمد. بنابراین گزینه 1 پاسخ صحیح می باشد.
به منظور تفهیم بیشتر موضوع شرط توازی و عمودی بودن دو خط می توانید ویدئو آموزشی را مشاهده کنید.
سوالات متداول
دو خط زمانی بر هم عمود هستند که شیب های آن ها، عکس قرینه یکدیگر باشد. در واقع حاصل ضرب شیب آن ها برابر با 1- شود.
دو خط زمانی با هم موازی هستند که شیب های آن ها با یکدیگر برابر باشد.





