در این فیلم آموزشی به موضوع احتمال هم شانس، فضای نمونه ای و پیشامد پرداخته شده است.
فضای نمونه ای، پیشامد و احتمال هم شانس
فضای نمونه ای: مجموعه ی شامل تمام حالت های ممکن در انجام یک آزمایش، فضای نمونه ای نامیده می شود.
فضای نمونه ای را با S نمایش می دهیم و به هر زیر مجموعه از آن یک پیشامد تصادفی می گوییم. مثلا در پرتاب دو تاس n(s)=36 و 236 پیشامد داریم.
مثال 1) در یک خانواده 4 فرزندی، فضای نمونه ای دارای چند عضو است؟
تعداد اعضای فضای نمونه ای برابر است با:
n(s)=24=16
زیرا هر کدام از فرزندان دارای دو حالت دختر یا پسر هستند.
مثال 2) در پرتاب 2 سکه و 3 تاس، تعداد اعضای فضای نمونه ای چند تاست؟
هر کدام از سکه ها دارای 2 حالت و هر کدام از تاس ها دارای 6 حالت هستند. لذا تعداد اعضای فضای نمونه ای برابر است با:
n(s)=2×2×6×6×6=22×63
مثال 3) جنسیت فرزندان یک خانواده 5 فرزندی 25 حالت دارد یعنی n(s)=32 پیشامد آنکه:
الف) 2 فرزند دختر داشته باشد؟
در این حالت 2 فرزند دختر و 3 فرزند پسر داریم. ابتدا جای 2 فرزند دختر را از بین 5 فرزند انتخاب می کنیم. بنابراین داریم:

نکته: در یک خانواده با n فرزند، تعداد حالاتی که تعداد دختران k باشد، (k n) ترکیب k از n است.
نکته: در یک خانواده با n فرزند، تعداد حالاتی که تعداد پسران k باشد، (k n) ترکیب k از n است.
ب) حداقل 2 فرزند دختر داشته باشد؟
در این صورت تعداد دختران برابر با 2 یا 3 یا 4 و یا 5 خواهد بود. همچنین تعداد حالاتی که حداقل 2 فرزند دختر داشته باشند، برابر است با کل حالات منهای تعداد حالات 0 و 1 دختر.

ج) حداکثر 2 فرزند دختر داشته باشد؟
در این صورت، یا صفر دختر یا 1 و یا 2 دختر خواهند داشت.
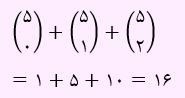
به مجموعه ی شامل تمام حالات ممکن در انجام یک آزمایش، فضای نمونه ای گفته خواهد شد.
نمونه تست احتمال هم شانس
در این بخش به منظور فهم بهتر موضوع به حل تست خواهیم پرداخت.
تست اول) در یک جعبه 4 مهره قرمز و 6 مهره سیاه داریم. اگر سه مهره به تصادف از کیسه خارج کنیم، پیشامد A آن است که هر سه مهره هم رنگ باشند و B پیشامد آن است که حداقل دو مهره قرمز باشند. کدام گزینه درست است؟
1- n(A)=24 و n(B)=36
2- n(A)=20 و n(B)=36
3- (A)=20 و n(B)=40
4- n(A)=24 و n(B)=40
گزینه 4 پاسخ صحیح می باشد.
تعداد کل مهره ها برابر با 10 خواهد بود. پیشامد A که هر سه مهره هم رنگ باشند، به صورت زیر خواهد بود. در واقع یا سه مهره سفید یا سه مهره سیاه هستند.

تعداد اعضای پیشامد B به صورت زیر خواهد بود:
در واقع یا دو مهره قرمز داریم یا هر سه مهره قرمز هستند.

برای آشنایی بیشتر با موضوع احتمال هم شانس، فضای نمونه ای، پیشامد و نمونه تست های آن می توانید ویدئو آموزشی را مشاهده کنید.
سوالات متداول
به مجموعه ی شامل تمام حالت های ممکن در انجام یک آزمایش، فضای نمونه ای گفته خواهد شد و آن را با S نشان می دهیم.
به هر زیر مجموعه از فضای نمونه ای یک پیشامد تصادفی گفته خواهد شد.
در یک خانواده با n فرزند، تعداد حالاتی که تعداد دختران k باشد، برابر با ترکیب k از n خواهد بود.





