در این فیلم آموزشی با موضوع تشابه مثلث ها و قضیه اساسی یا اصلی تشابه آشنا خواهید شد.
قضیه اساسی تشابه
قضیه اساسی تشابه: اگر خطی موازی یکی از اضلاع مثلث، دو ضلع دیگر را قطع کند در این صورت مثلث کوچکی که به وجود می آید با مثلث بزرگ اولیه متشابه است. در حقیقت در شکل زیر، روابط بیان شده برقرار است.

عکس قضیه: اگر فرض و حکم یک قضیه را جا به جا کنیم آنچه حاصل می شود ” عکس قضیه” است. عکس یک قضیه می تواند درست یا نادرست باشد.
قضیه اساسی تشابه بیان می کند اگر خطی موازی یکی از اضلاع مثلث، دو ضلع دیگر را قطع کند در این صورت مثلث به وجود آمده با مثلث بزرگ اولیه متشابه است.
حالت های تشابه دو مثلث
حالت های تشابه دو مثلث شامل موارد زیر می باشد:
- اگر دو زاویه از مثلثی با دو زاویه از مثلث دیگر برابر باشند، دو مثلث متشابه اند.
- اگر اندازه های دو ضلع از مثلثی با اندازه های دو ضلع از مثلث دیگر متناسب باشند و زاویه بین آن ها برابر باشند، دو مثلث متشابه اند.
- اگر اندازه های سه ضلع از مثلثی با اندازه های سه ضلع از مثلث دیگر متناسب باشند، دو مثلث متشابه اند.
حالت 1 بیشترین کاربرد و استفاده را در تست های کنکور سراسری دارد.
مثال: در هر یک از شکل های زیر مثلث ABC با مثلث A’B’C مشابه است.

به نمونه تست زیر توجه کنید:
تست) با توجه به شکل مقابل، حاصل OB+A’B’ 1 کدام است؟
- 40
- 41
- 42
- 43
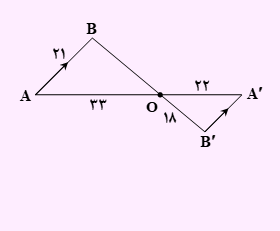
گزینه 2 پاسخ صحیح می باشد.
در شکل بالا، دو زاویه o1 و o2 با یکدیگر برابرند. چون این دو زاویه متقابل به راس هستند. از توازی AB با A’B’ 1 ، می توان فهید دو زاویه B1 و B’1 با هم برابر می باشند. همچنین دو زاویه A1 و A’1 نیز با یکدیگر مساوی هستند. بنابراین دو مثلث OAB و OA’B’ 1 با یکدیگر مشابه اند. لذا نسبت تناسب را به صورت زیر می نویسیم.
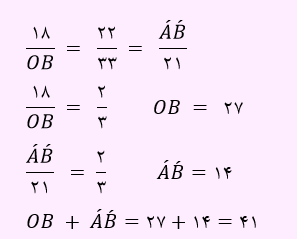
بنابراین حاصل عبارت خواسته شده برابر با 41 می باشد.
برای یادگیری بیشتر موضوع قضیه اساسی تشابه و نمونه تست های آن ویدئو آموزشی را مشاهده کنید.
سوالات متداول
قضیه اساسی تشابه بیان می کند، اگر خطی موازی یکی از اضلاع مثلث باشد و دو ضلع دیگر را قطع کند، آن گاه مثلث کوچکی که در اثر این خط به وجود می آید با مثلث بزرگ اولیه متشابه می باشد.
دو مثلث در حالت های زیر با یکدیگر متشابه هستند.
- اگر دو زاویه از یک مثلث با دو زاویه از مثلث دیگر مساوی باشند، آن گاه دو مثلث متشابه خواهند بود.
- اگر اندازه های دو ضلع از یک مثلث با اندازه های دو ضلع از مثلث دیگر تناسب داشته باشند و زاویه بین آن ها مساوی باشند، در این صورت دو مثلث متشابه می باشند.
- اگر اندازه های سه ضلع از یک مثلث با اندازه های سه ضلع از مثلث دیگر متناسب باشند، در این حالت دو مثلث متشابه هستند.
خیر. در این حالت نمی توان گفت لزوما دو مثلث با یکدیگر متشابه اند. اگر ضلع سوم این دو مثلث نیز با یکدیگر متناسب باشند، در آن صورت دو مثلث متشابه اند. یا اگر زاویه بین دو ضلعی که متناسب اند با یکدیگر در دو مثلث برابر باشد، آن گاه دو مثلث متشابه خواهند بود.





