در این فیلم آموزشی به موضوع روابط طولی در مثلث قائم الزاویه و قضیه فیثاغورث خواهیم پرداخت.
قضیه فیثاغورث و روابط طولی در مثلث قائم الزاویه
برخی روابط طولی در مثلث قائم الزاویه به صورت زیر می باشند:
در هر مثلث قائم الزاویه، ارتفاع وارد بر وتر، دو مثلث قائم الزاویه به وجود می آورد که این دو مثلث با هم و با مثلث اصلی متشابه اند. در واقع در شکل زیر، روابط بیان شده برقرار می باشد.

تذکر: دو رابطه زیر نیز در مثلث قائم الزاویه برقرار است:
به رابطه اول، رابطه فیثاغورث گفته خواهد شد.

رابطه فیثاغورث بیان می کند توان دوم وتر برابر با مجموع توان دوم دو ضلع دیگر مثلث قائم الزاویه است.
نمونه تست قضیه فیثاغورث و روابط طولی در مثلث قائم الزاویه
به نمونه تست های زیر توجه کنید:
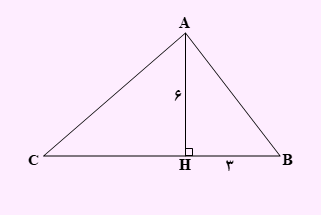
تست ) با توجه به شکل مقابل طول AC کدام است؟
- 5√5
- 5√6
- 5√7
- 5√8
گزینه 2 پاسخ صحیح می باشد.
چون این مثلث قائم الزاویه است، رابطه زیر برقرار می باشد.
AH2=BH.CH 36=3×CH CH=12
حال در مثلث ACH قضیه فیثاغورث را می نویسیم.
AC2=AH2+CH2=62+122=62(1+22) AC=6√5
لذا طول AC برابر است با 5√6
به نمونه تست دوم توجه کنید:
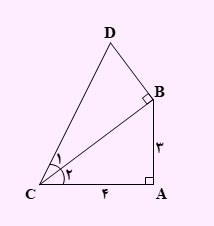
تست) با توجه به شکل مقابل، طول CD چقدر است؟ ( زاویه c1 و c2 با یکدیگر برابرند)
- 6
- 8
- 25/4
- 13/2
گزینه 3 پاسخ صحیح می باشد.
چون زاویه c1 و c2 با یکدیگر برابرند، بنابراین خط CB نیمساز زاویه C است. ابتدا از نقطه B یک خط عمود بر DC وارد می کنیم. چون نقطه B روی نمیساز قرار دارد، حتما عمود BH با BA برابر می باشد. زیرا هر نقطه روی نمیساز از دو ضلع زاویه به یک فاصله است. بنابراین طول BH مساوی با 3 خواهد بود. طبق قضیه فیثاغورث برای مثلث ABC، اندازه BC برابر با 5 است. همچنین مجددا با توجه به قضیه فیثاغورث برای مثلث CHB، اندازه CH نیز مساوی با 4 می باشد.
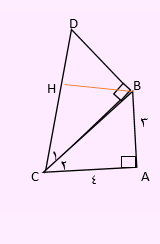
حال از رابطه زیر برای محاسبه طول CD استفاده خواهیم کرد.
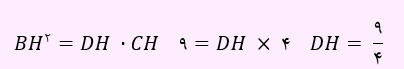
بنابرای طول CD مساوی است با 9/4+4 . یعنی طول CD برابر با 25/4 خواهد بود.
در این جلسه رابطه فیثاغورث و موارد مربوط به آن بررسی گردید. شما می توانید جهت آموزش بیشتر ویدئوی این جلسه را مشاهده نمایید.
سوالات متداول
در هر مثلث قائم الزاویه مربع وتر برابر است با مجموع مربع دو ضلع دیگر. به این رابطه که در مثلث قائم الزاویه همواره برقرار است، قضیه فیثاغورث گفته خواهد شد.
لازم به ذکر است، در هر مثلث قائم الزاویه، مربع ارتفاع وارد بر وتر برابر است با ضرب قطعاتی که روی وتر ایجاد می شود.
در هر مثلث قائم الزاویه، مربع هر ضلع برابر است با ضرب وتر در تصویر آن ضلع در وتر .





