در این فیلم آموزشی با قوانین مجموعه ها شامل قانون جا به جایی، شرکت پذیری، توزیع پذیری و قانون دمورگان، نکات و تست جبر مجموعه ها آشنا خواهید شد.
قوانین مجموعه ها
قوانین مجموعه ها : قوانین جا به جایی، شرکت پذیری و توزیع پذیری در اجتماع و اشتراک مجموعه ها به صورت زیر می باشد:
A ∪B=B ∪A
A ∩B=B ∩A
قانون بالا، قانون جا به جایی می باشد.
A ∩( B ∩C)=( A ∩B)∩C
A ∪(B ∪C)=(A ∪B)∪C
قانون بالا، شرکت پذیری نام دارد.
A ∪(B ∩C)=(A ∪B)∩(A ∪C)
A ∩(B ∪C)=(A ∩B)∪(A ∩C)
به قانون بالا، توزیع پذیری گفته خواهد شد.
(A∪B)’=A’∩B’
(A∩B)’=A’∪B’
قانون دمورگان به شکل بالا می باشد.
A ∪(A∩B)=A
A ∩(A ∪B)=A
به قوانین بالا، قانون جذب گفته خواهد شد.
قوانین متمم مجموعه ها به صورت زیر است:
A ∪ A ́ =U
A ∩ A ́= ∅
قوانین مجموعه های تهی و مرجع به شکل زیر خواهد بود:
A∪U=U
A∩U=A
A∪∅ =A
A∩∅= ∅
(∅) ́=U
U ́= ∅
فرمول اساسی تفاضل دو مجموعه به حالت زیر است:
A-B=A ∩B ́=A-(A∩B)
اجتماع و اشتراک مجموعه ها شامل قانون جا به جایی می باشد.
نمونه تست قوانین مجموعه ها
به نمونه تست اول دقت کنید:
تست اول) ساده شده عبارت ‘𝐴−𝐵)∪ (𝐴 ∪𝐵)) کدام است؟
الف) ∅
ب) U
ج) ‘A
د) ‘B
گزینه د پاسخ صحیح می باشد.
عبارت مورد نظر به صورت زیر ساده خواهد شد:
تست دوم در مورد ساده شدن عبارات جبری می باشد:
تست دوم) ساده شده عبارت [ A ∩(A ́ ∪B)]∪[ B ∩(A ́ ∪ B ́ )] کدام است؟
الف) ∅
ب) U
ج) A
د) B
گزینه د پاسخ صحیح می باشد.
ابتدا قسمت اول عبارت A ∩(A ́ ∪B) را به صورت زیر ساده خواهیم کرد:
حال قسمت دوم عبارت یعنی B ∩(A ́ ∪ B ́ ) را ساده می نمائیم.
بنابراین عبارت به صورت زیر ساده خواهد شد:
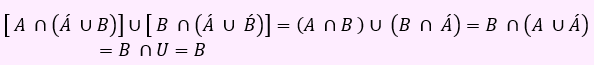
به منظور مشاهده نمونه تست های بیشتر در مورد موضوع قوانین مجموعه ها ویدئو آموزشی را مشاهده کنید.
سوالات متداول
اگر متمم در اجتماع اثر کند، آن را تبدیل به اشتراک خواهد کرد و اگر متمم در اشتراک اثر کند، آن را به اجتماع تبدیل می کند.
اشتراک هر مجموعه با متممش برابر با تهی و اجتماع آن ها مساوی با مجموعه مرجع یعنی U خواهد شد.
فرض کنید A و B دو مجموعه دلخواه باشند، فرمول اساسی تفاضل این دو مجموعه به صورت زیر می باشد:
A-B=A ∩B ́=A-(A∩B)






گگگوود
عالی بود ممنون
تو کلیپ آموزشی اخرین تست میشد گزینه ۳.
ممنون از آمورشاتون